题目内容
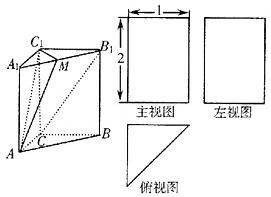 如图,三棱柱A1B1C1-ABC的三视图中,主视图和左视图是全等的矩形,俯视图是等腰直角三角形,已知点M式A1B1的中点.
如图,三棱柱A1B1C1-ABC的三视图中,主视图和左视图是全等的矩形,俯视图是等腰直角三角形,已知点M式A1B1的中点.(I)求证B1C∥平面AC1M;
(Ⅱ)设AC与平面AC1M的夹角为θ,求sinθ.
分析:由题可知,三棱柱A1B1C1-ABC的三视图中,主视图和左视图是全等的矩形,俯视图是等腰直角三角形,要证B1C∥平面AC1M,利用线线平行,要求sinθ利用平面法向量,求解即可.
解答: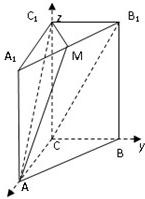 解:(Ⅰ)由三视图可知三棱柱A1B1C1-ABC为直三棱柱,
解:(Ⅰ)由三视图可知三棱柱A1B1C1-ABC为直三棱柱,
侧棱长为2,底面为等腰直角三角形,AC=BC=1如图建立空间直角坐标系C-xyz,
则C(0,0,0),C1(0,0,2),A(1,0,0),B1(0,1,2),
A1(1,0,2),∵M为A1B1为中点,∴M(
,
,2)
=(0,1,2),
=(-
,
,2),
=(
,
,0)
∴
=
+
∴
∥面AC1M,又因为CB1?面AC1M
∴CB1∥面AC1M
(Ⅱ)设平面AC1M的一个法向量为
=(x,y,z)
,
令z=1,则x=2,y=-2,∴
=(2,-2,1)
又
=(-1,0,0)
则sinB-|cos<
,
>|=|
|=
 解:(Ⅰ)由三视图可知三棱柱A1B1C1-ABC为直三棱柱,
解:(Ⅰ)由三视图可知三棱柱A1B1C1-ABC为直三棱柱,侧棱长为2,底面为等腰直角三角形,AC=BC=1如图建立空间直角坐标系C-xyz,
则C(0,0,0),C1(0,0,2),A(1,0,0),B1(0,1,2),
A1(1,0,2),∵M为A1B1为中点,∴M(
| 1 |
| 2 |
| 1 |
| 2 |
| CE1 |
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
| C1M |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| CB1 |
| AM |
| C1M |
| CB1 |
∴CB1∥面AC1M
(Ⅱ)设平面AC1M的一个法向量为
| m |
|
令z=1,则x=2,y=-2,∴
| m |
又
| AC |
则sinB-|cos<
| m |
| AC |
| ||||
|
|
| 2 |
| 3 |
点评:本题考查学生的空间想象能力,以及对空间直角坐标系的使用,是中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
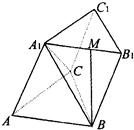 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.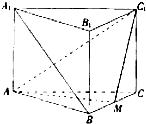 如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=BC=2AA1,∠ABC=90°,M是BC中点.
如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=BC=2AA1,∠ABC=90°,M是BC中点.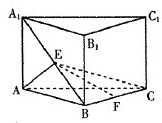 如图,三棱柱ABC-A1B1 C1中,侧棱AA1⊥平面ABC,AB=BC=AA1=2,AC=2
如图,三棱柱ABC-A1B1 C1中,侧棱AA1⊥平面ABC,AB=BC=AA1=2,AC=2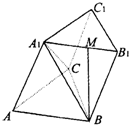 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.