题目内容
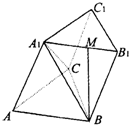 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧面ABB1A1是菱形且垂直于底面,∠A1AB=60°,M是A1B1的中点.(1)求证:BM⊥AC;
(2)求二面角B-B1C1-A1的正切值;
(3)求三棱锥M-A1CB的体积.
分析:(1)根据△BA1B1是等边三角形,BM⊥A1B1 ,面ABB1A1垂直于底面,可得BM⊥面 A1B1C1 ,从而得到BM⊥面ABC,
BM⊥AC.
(2)作MN⊥B1C1 ,证明∠MNB为二面角B-B1C1-A1的平面角,由Rt△MNB中,tan∠MNB=
,运算求得结果.
(3)三棱锥M-A1CB的体积 VM-A1CB=VC-A1MB=
×(
• A1M•BM)•h,把点C到面A1BM的距离h即等边
三角形ABC的高
a,代入公式运算求得结果.
BM⊥AC.
(2)作MN⊥B1C1 ,证明∠MNB为二面角B-B1C1-A1的平面角,由Rt△MNB中,tan∠MNB=
| BM |
| MN |
(3)三棱锥M-A1CB的体积 VM-A1CB=VC-A1MB=
| 1 |
| 3 |
| 1 |
| 2 |
三角形ABC的高
| ||
| 2 |
解答:解:(1)∵侧面ABB1A1是菱形,∠A1AB=60°,M是A1B1的中点,
∴△BA1B1是等边三角形,BM⊥A1B1 .
再由面ABB1A1垂直于底面,可得BM⊥面 A1B1C1 .
故BM⊥面ABC,∴BM⊥AC.
(2)作MN⊥B1C1 ,由三垂线定理可得BN⊥B1C1 ,故∠MNB为二面角B-B1C1-A1的平面角.
MN=BMsin60°=
×
=
a,BM=BB1sin60°=
a.
Rt△MNB中,tan∠MNB=
=2.
所求二面角的正切值是2.
(3)三棱锥M-A1CB的体积 VM-A1CB=VC-A1MB=
×(
• A1M•BM)•h,
而h是点C到面A1BM的距离,即等边三角形ABC的高为
a,
∴三棱锥M-A1CB的体积为
×(
•
•
)•
a=
a3.
∴△BA1B1是等边三角形,BM⊥A1B1 .
再由面ABB1A1垂直于底面,可得BM⊥面 A1B1C1 .
故BM⊥面ABC,∴BM⊥AC.
(2)作MN⊥B1C1 ,由三垂线定理可得BN⊥B1C1 ,故∠MNB为二面角B-B1C1-A1的平面角.
MN=BMsin60°=
| a |
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
Rt△MNB中,tan∠MNB=
| BM |
| MN |
所求二面角的正切值是2.
(3)三棱锥M-A1CB的体积 VM-A1CB=VC-A1MB=
| 1 |
| 3 |
| 1 |
| 2 |
而h是点C到面A1BM的距离,即等边三角形ABC的高为
| ||
| 2 |
∴三棱锥M-A1CB的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| a |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 16 |
点评:本题考查证明线线垂直的方法,求二面角的大小的方法,求棱锥的体积,体现了转化的数学思想,找出二面角的平面角并
求出棱锥的高,是解题的关键和难点.
求出棱锥的高,是解题的关键和难点.

练习册系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=