Question

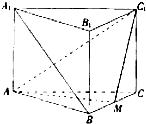如图，三棱柱ABC-A₁B₁C₁中，侧棱与底面垂直，AB=BC=2AA₁，∠ABC=90°，M是BC中点．
（Ⅰ）求证：A₁B∥平面AMC₁；
（Ⅱ）求直线CC₁与平面AMC₁所成角的正弦值；
（Ⅲ）试问：在棱A₁B₁上是否存在点N，使AN与MC₁成角60°？若存在，确定点N的位置；若不存在，请说明理由．

Answer 1

分析：（Ⅰ）证明线面平行，可以利用线面平行的判定定理，只要证明 A₁B∥OM可；
（Ⅱ）可判断BA，BC，BB₁两两垂直，建立空间直角坐标系，用坐标表示点与向量，求得平面AMC₁的法向量、直线CC₁的阐释，向量，代入向量夹角公式，可求直线CC₁与平面AMC₁所成角的正弦值；
（Ⅲ）假设存在满足条件的点N，根据AN与MC₁成60°角，利用向量的数量积，可得结论．

解答：证明：（Ⅰ）连接A₁C，交AC₁于点O，连接OM．
∵ABC-A₁B₁C₁是直三棱柱，
∴四边形ACC₁A₁为矩形，O为A₁C的中点．
又∵M为BC中点，
∴OM为△A₁BC中位线，
∴A₁B∥OM，
∵OM?平面AMC₁，A₁B?平面AMC₁，
所以 A₁B∥平面AMC₁．…（4分）
解：（Ⅱ）由ABC-A₁B₁C₁是直三棱柱，且∠ABC=90°，
故BA，BC，BB₁两两垂直．可建立如图空间直角坐标系B-xyz．
设BA=2，则B（0，0，0），C（2，0，0），A（0，2，0），C₁（2，0，1），M（1，0，0）．
则

AM

=（1，-2，0），

AC1

=（2，-2，1），
设平面AMC₁的法向量为

m

=（x，y，z），则有

m • AM =0 m • AC1 =0

，即

x-2y=0 2x-2y+z=0

所以取y=1，得

m

=（2，1，-2）．
又∵

CC1

=（0，0，1）
∴直线CC₁与平面AMC₁所成角θ满足
sinθ=

| CC1 • m |

| CC1 |•| m |

=

2

3

故直线CC₁与平面AMC₁所成角的正弦值为

2

3

解：（Ⅲ）假设存在满足条件的点N．
∵N在线段A₁B₁上，A₁（0，2，1），B₁（0，0，1），
故可设N（0，λ，1），其中0≤λ≤2．
∴

AN

=（0，λ-2，1），

MC1

=（1，0，1）．
∵AN与MC₁成60°角，
∴

| DC1 • AN |

| DC1 |•| AN |

=

1

(λ-2)2+1 • 2

=

1

2

．
即，解得λ=1，或λ=3（舍去）．
所以当点N为线段A₁B₁中点时，AN与MC₁成60°角．…（12分）

点评：本题考查线面平行，考查线面夹角，考查存在性问题的探究，解题的关键是掌握线面平行的判定定理，正确运用向量的方法解决线面角、线线角．