题目内容
18.在△ABC中,点M是边BC上的一点,BM=3,AC=2$\sqrt{10}$,∠B=45°,cos∠BAM=$\frac{3\sqrt{10}}{10}$.(I)求线段AM的长度;
(Ⅱ)求线段MC的长度.
分析 (I)在△ABM中使用正弦定理解出AM;
(II)求出cos∠AMB,得出cos∠AMC,在△AMC中使用余弦定理列方程解出MC.
解答 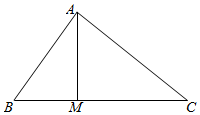 解:(I)∵cos∠BAM=$\frac{3\sqrt{10}}{10}$,∴sin∠BAM=$\frac{\sqrt{10}}{10}$.
解:(I)∵cos∠BAM=$\frac{3\sqrt{10}}{10}$,∴sin∠BAM=$\frac{\sqrt{10}}{10}$.
在△ABM中,由正弦定理得:$\frac{BM}{sin∠BAM}=\frac{AM}{sinB}$,即$\frac{3}{\frac{\sqrt{10}}{3}}=\frac{AM}{\frac{\sqrt{2}}{2}}$,
解得AM=3$\sqrt{5}$.
(II)cos∠AMB=-cos(∠BAM+∠B)=sin∠BAMsinB-cos∠BAMcosB=$\frac{\sqrt{10}}{10}×\frac{\sqrt{2}}{2}-\frac{3\sqrt{10}}{10}×\frac{\sqrt{2}}{2}$=-$\frac{\sqrt{5}}{5}$.
∵∠AMB+∠AMC=π,
∴cos∠AMC=-cos∠AMB=$\frac{\sqrt{5}}{5}$.
在△AMC中,由余弦定理得cos∠AMC=$\frac{A{M}^{2}+M{C}^{2}-A{C}^{2}}{2AM•MC}$,
即$\frac{\sqrt{5}}{5}$=$\frac{45+M{C}^{2}-40}{6\sqrt{5}MC}$,解得MC=1或MC=5.
点评 本题考查了正弦定理,余弦定理解三角形,属于中档题.

练习册系列答案
相关题目
13.已知(m+x)7=a0+a1(1-x)+a2(1-x)2+…+a7(1-x)7,a0-a1+a2-a3+…-a7=37,则|a0|+|a1|+|a2|+…+|a7|=( )
| A. | 1 | B. | 2187 | C. | 2188 | D. | -2187 |
17.下列说法正确的是( )
| A. | P(B|A)<P(AB) | B. | P(B|A)=$\frac{P(B)}{P(A)}$是可能的 | ||
| C. | 0<P(B|A)<1 | D. | P(A|A)=0 |
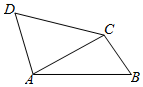 如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.
如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.