题目内容
14．给出下列命题：①向量$\overrightarrow{AB}$与$\overrightarrow{BA}$是相等向量；②共线的单位向量是相等向量；③模为零的向量与任一向量共线；④两平行向量所在直线互相平行．其中不正确的是（ ）| A． | ①②③ | B． | ②③④ | C． | ①②④ | D． | ①②③④ |
分析 根据平面向量的基本概念，对命题①②③④的真假性进行判断即可．
解答 解：对于①，向量$\overrightarrow{AB}$与$\overrightarrow{BA}$是相反向量，不一定是相等向量，①错误；
对于②，共线的单位向量不一定是相等向量，也可能是相反向量，②错误；
对于③，模为零的向量是零向量，它与任一向量共线，③正确；
对于④，两平行向量所在直线不一定互相平行，也可能重合，④错误；
综上，其中不正确的是①②④．
故选：C．
点评 本题考查了平面向量的基本概念与应用问题，是基础题．
练习册系列答案
相关题目
4．已知A，B，C三点在球O的表面，△ABC是边长为5正三角形，球面上另外一点D到A，B，C三点的距离分别是3，4，5，则球O的表面积是（ ）
| A． | $\frac{100π}{3}$ | B． | $\frac{400π}{3}$ | C． | 100π | D． | 400π |
5．
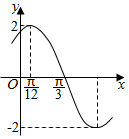函数$f（x）=Asin（{ωx+ϕ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，
求（Ⅰ）函数f（x）的解析式；
（Ⅱ）函数y=Acos（ωx+ϕ）的单调递增区间．
函数$f（x）=Asin（{ωx+ϕ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，求（Ⅰ）函数f（x）的解析式；
（Ⅱ）函数y=Acos（ωx+ϕ）的单调递增区间．
2．已知$sin（-α）=\frac{{\sqrt{5}}}{3}$，则$cos（\frac{π}{2}+α）$的值为（ ）
| A． | $\frac{2}{3}$ | B． | $-\frac{2}{3}$ | C． | $\frac{{\sqrt{5}}}{3}$ | D． | $-\frac{{\sqrt{5}}}{3}$ |
19．某市电子认证审查流程图如图：
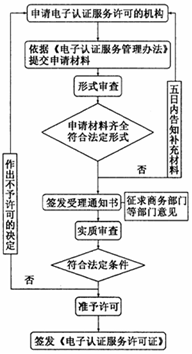
则有几处审查可能不被通过的环节（ ）
则有几处审查可能不被通过的环节（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 0 |
