题目内容
如图,空间四边形 的对棱
的对棱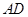 、
、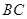 成
成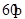 的角,且
的角,且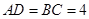 ,平行于
,平行于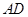 与
与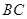 的截面分别交
的截面分别交 、
、 、
、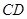 、
、 于
于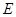 、
、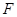 、
、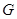 、
、 .
.
(1)求证:四边形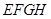 为平行四边形;
为平行四边形;
(2)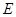 在
在 的何处时截面
的何处时截面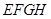 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
(1)利用线面平行的性质得到线线平行,然后再利用平行四边形的定义即可证明.(2)当E为AB的中点时,截面面积最大, ,
,
解析试题分析:(1) 平面
平面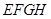 ,
, 平面
平面 ,
,
平面 平面
平面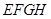
 ,
, .同理
.同理 ,
, ,同理
,同理 ,
, 四边形
四边形 为平行四边形.
为平行四边形.
(2)
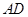 与
与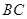 成
成 角,
角,
 或
或 ,
,
当E为AB的中点时,截面面积最大, ,
,
考点:本题考查了线面平行的性质及平行四边形的概念、面积
点评:证明两直线平行的方法有:①依定义采用反证法;②利用公理4;③线面平行的性质定理;④面面平行的性质定理

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
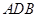 是圆
是圆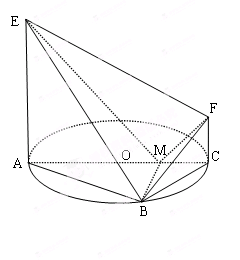
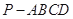 中,侧面
中,侧面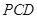
 底面
底面 ,
, ,底面
,底面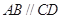 ,
,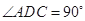 ,
,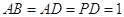 ,
,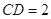 .
.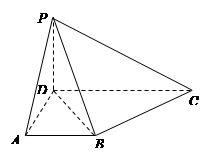
 平面
平面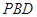 ;
; 为侧棱
为侧棱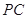 上一点,
上一点,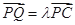 ,试确定
,试确定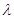 的值,使得二面角
的值,使得二面角 为
为 .
.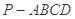 中,底面
中,底面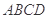 为正方形,
为正方形,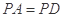
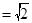 ,
,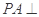 平面
平面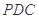 ,
,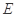 为棱
为棱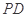 的中点.
的中点.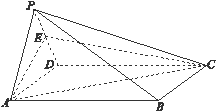
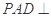 平面
平面 ;
; 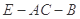 的余弦值.
的余弦值. 到平面
到平面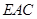 的距离.
的距离.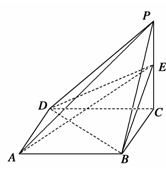
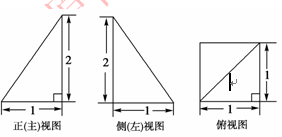
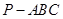 ,底面
,底面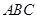 为边长为
为边长为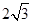 的正三角形,平面
的正三角形,平面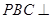 平面
平面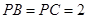 ,
,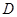 为
为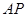 上一点,
上一点,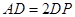 ,
,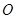 为底面三角形中心.
为底面三角形中心. 
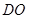 ∥面
∥面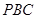 ;
;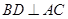 ;
;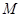 为
为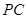 中点,求二面角
中点,求二面角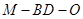 的余弦值.
的余弦值.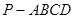 中,
中,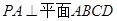 ,
,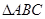 是正三角形,
是正三角形,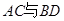 的交点
的交点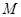 恰好是
恰好是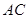 中点,又
中点,又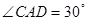 ,
,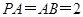 ,点
,点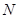 在线段
在线段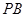 上,且
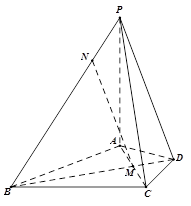
上,且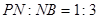 .
.
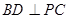 ;
;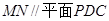 ;
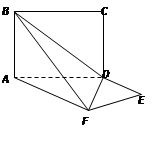
;
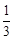 ,求AB的长.
,求AB的长.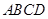 ,其边长为2,
,其边长为2,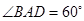 ,
,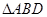 绕着
绕着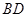 顺时针旋转
顺时针旋转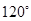 得到
得到 ,
,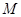 是
是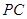 的中点.
的中点.
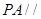 平面
平面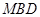 ;
;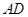 与平面
与平面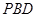 所成角的正弦值.
所成角的正弦值.