题目内容
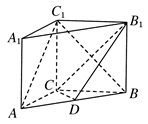
如图所示,已知正方形 和矩形
和矩形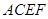 所在的平面互相垂直,
所在的平面互相垂直,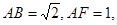
 是线段
是线段 的中点。
的中点。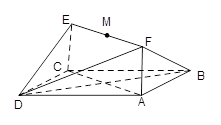
(1)证明: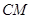 ∥平面
∥平面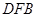
(2)求异面直线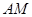 与
与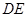 所成的角的余弦值。
所成的角的余弦值。
(1)建立空间直角坐标系,用坐标表示点与向量,证明CM与平面BDF的法向量垂直,即可证得结论;
(2)
解析试题分析:(1)证明:建立如图所示的空间直角坐标系,则 …(2分)
…(2分)
设平面DBF的一个法向量为 ,则
,则 ,
,
∴
取 ,
,
得平面DBF的一个法向量为 ,…(6分)
,…(6分)
因为 ,
,
所以 ,
,
又因为直线CM?平面DBF内,所以CM∥平面BDF.…(6分)
(2)结合上一问可知求异面直线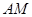 与
与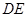 所成的角的余弦值,只要确定出向量AM和向量DE的坐标即可,结合平面向量的夹角公式来得到为
所成的角的余弦值,只要确定出向量AM和向量DE的坐标即可,结合平面向量的夹角公式来得到为
考点:线面平行,异面直线的角
点评:本题考查线面平行,考查面面角,解题的关键是建立空间直角坐标系,用坐标表示点与向量,利用向量的数量积求解

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
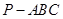 ,底面
,底面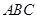 为边长为
为边长为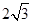 的正三角形,平面
的正三角形,平面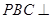 平面
平面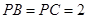 ,
,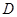 为
为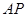 上一点,
上一点,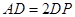 ,
,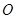 为底面三角形中心.
为底面三角形中心. 
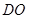 ∥面
∥面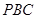 ;
;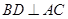 ;
;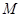 为
为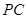 中点,求二面角
中点,求二面角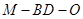 的余弦值.
的余弦值.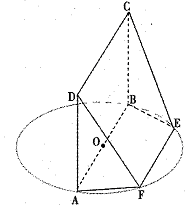
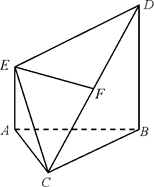
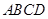 ,其边长为2,
,其边长为2,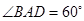 ,
,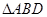 绕着
绕着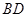 顺时针旋转
顺时针旋转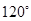 得到
得到 ,
,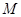 是
是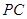 的中点.
的中点.
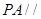 平面
平面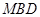 ;
;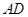 与平面
与平面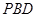 所成角的正弦值.
所成角的正弦值.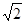 ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.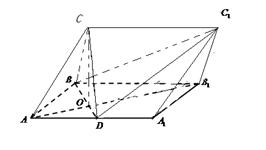
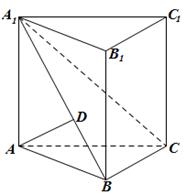
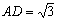 ,AB=BC=2,P为AC中点,求三棱锥
,AB=BC=2,P为AC中点,求三棱锥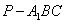 的体积。
的体积。 .
.