题目内容
在正方体 中,过对角线
中,过对角线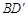 的一个平面交棱
的一个平面交棱 于E,交棱
于E,交棱 于F,则:①四边形
于F,则:①四边形 一定是平行四边形;②四边形
一定是平行四边形;②四边形 有可能是正方形;③四边形
有可能是正方形;③四边形 有可能是菱形;④四边形
有可能是菱形;④四边形 有可能垂直于平面
有可能垂直于平面 .
.
其中所有正确结论的序号是 .
①③④
解析试题分析:对于①,根据面面平行的性质易知 ,所以四边形
,所以四边形 一定是平行四边形,①正确;对于②,四边形
一定是平行四边形,①正确;对于②,四边形 不可能为正方形;假设
不可能为正方形;假设 为正方形,则
为正方形,则 ,而
,而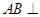 平面
平面 ,所以
,所以 ,从而由线面垂直的判定可得
,从而由线面垂直的判定可得 平面
平面 ,故点
,故点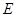 与点
与点 重合,此时点
重合,此时点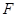 与点
与点 重合(如下图(2)),而这时四边形
重合(如下图(2)),而这时四边形 就是四边形
就是四边形 ,明显
,明显 ,假设不正确,所以四边形
,假设不正确,所以四边形 不可能为正方形;对于③④都是正确的,如下图(1),当点
不可能为正方形;对于③④都是正确的,如下图(1),当点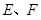 分别为
分别为 的中点时,显然该平行四边形
的中点时,显然该平行四边形 的各棱长都相等,所以③正确,此时也有
的各棱长都相等,所以③正确,此时也有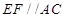 ,而不难证明
,而不难证明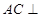 平面
平面 ,所以
,所以 平面
平面 ,由面面垂直的判定可知,此时面
,由面面垂直的判定可知,此时面 面
面 ,综上可知,①③④所表示的结论都正确.
,综上可知,①③④所表示的结论都正确.

考点:1.空间中的平行问题;2.空间中的垂直问题.

练习册系列答案
相关题目
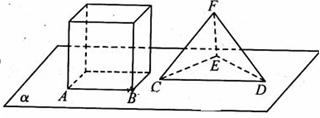
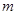 ,
,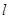 和平面
和平面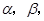 且
且 ,给出下列四个命题:
,给出下列四个命题: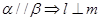 ②
②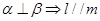 ③
③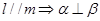 ④
④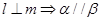
 与直线
与直线 的距离为 .
的距离为 . 中,
中,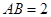 ,点
,点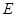 为
为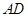 的中点,点
的中点,点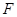 在
在 上,若
上,若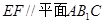 ,则线段
,则线段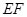 的长度等于______.
的长度等于______.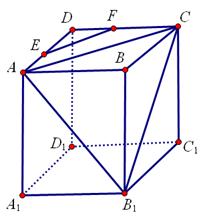
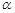 ,
,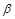 ,
, 是三个不同的平面,给出下列命题:
是三个不同的平面,给出下列命题: 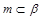 ,
,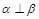 ,则
,则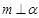 ;
;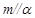 ,
,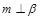 ,则
,则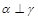 ,则
,则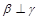 ;
;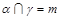 ,
,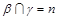 ,
,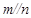 ,则
,则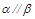 .
. 平面
平面 ,在折起后形成的三棱锥D-ABC中,给出下列三个命题:
,在折起后形成的三棱锥D-ABC中,给出下列三个命题: 是等边三角形;
是等边三角形;
