题目内容
已知单位向量 ,
, 的夹角为120°,当|
的夹角为120°,当|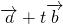 |(t∈R)取得最小值时t=________.
|(t∈R)取得最小值时t=________.

分析:根据单位向量模为1,可得
 •
• =-
=- .因此算出|
.因此算出|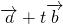 |2=t2-t+1,结合二次函数的图象与性质即可得到当|
|2=t2-t+1,结合二次函数的图象与性质即可得到当|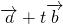 |取得最小值时t=
|取得最小值时t= ,得到本题的答案.
,得到本题的答案.解答:∵单位向量
 ,
, 的夹角为120°,
的夹角为120°,∴
 •
• =|
=| |•|
|•| |cos120°=-
|cos120°=-
因此,|
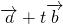 |2=
|2= +2t
+2t •
• +t2
+t2 =t2-t+1=(t-
=t2-t+1=(t- )2+
)2+
∴当且仅当t=
 时,|
时,|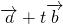 |2的最小值为
|2的最小值为 ,此时|
,此时|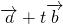 |取得最小值
|取得最小值
故答案为:

点评:本题给出夹角为120°的单位向量
 ,
, ,求当|
,求当|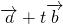 |取得最小值时t的值,着重考查了单位向量、向量的数量积和二次函数的图象与性质等知识,属于基础题.
|取得最小值时t的值,着重考查了单位向量、向量的数量积和二次函数的图象与性质等知识,属于基础题. 
练习册系列答案
相关题目
 ,
, 的夹角为60°,则
的夹角为60°,则 。
。 ,
, 的夹角为60°,则
的夹角为60°,则 。
。 和
和 的夹角为90°,点C在以O为圆心的圆弧AB(含端点)上运动,若
的夹角为90°,点C在以O为圆心的圆弧AB(含端点)上运动,若 ,则xy的取值范围是 .
,则xy的取值范围是 . ,
, 的夹角为120°,当|2
的夹角为120°,当|2 +x
+x |(x∈R)取得最小值时x= .
|(x∈R)取得最小值时x= . ,
, 的夹角为
的夹角为 ,且
,且 =2
=2 +k
+k ,
, =
= +
+ ,
, =
= -2
-2 ;
;