题目内容
f（x）=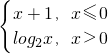
，函数y=f[f（x）]+1的所有零点所构成的集合为________．
分析：函数y=f[f（x）]+1的零点，即求方程f[f（x）]+1=0的解，下面分：当x≤-1，-1＜x≤0，0＜x≤1，x＞1时4中情况，分别代入各自的解析式求解即可．
解答：当x≤-1时，f（x）=x+1≤0，
∴f[f（x）]+1=x+1+1+1=0，∴x=-3；
当-1＜x≤0时，f（x）=x+1＞0，
∴f[f（x）]+1=log2（x+1）+1=0，∴x=-
；当0＜x≤1时，f（x）=log2x≤0，
∴f[f（x）]+1=log2x+1+1=0，∴x=
；当x＞1时，f（x）=log2x＞0，
∴f[f（x）]+1=log2（log2x）+1=0，∴x=
所以函数y=f[f（x）]+1的所有零点所构成的集合为：{
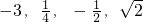}故答案为：{
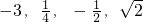}．点评：本题考查函数的零点、方程的解法以及分类讨论的思想．属基础题．
练习册系列答案
相关题目