题目内容
10.曲线$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1与曲线$\frac{x^2}{25t}+\frac{y^2}{9t}=1({t>0})$的( )| A. | 长轴长相等 | B. | 短轴长相等 | C. | 离心率相等 | D. | 焦距相等 |
分析 根据题意,由椭圆的方程计算可得两个椭圆的长轴长、短轴长,焦距、离心率,比较即可得答案.
解答 解:曲线$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1与曲线$\frac{x^2}{25t}+\frac{y^2}{9t}=1({t>0})$都表示椭圆,
对于$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,其中a=$\sqrt{25}$=5,b=$\sqrt{9}$=3,则有c=$\sqrt{25-9}$=4,
则其长轴长2a=10,短轴长2b=6,焦距2c=8,离心率e=$\frac{c}{a}$=$\frac{4}{5}$;
对于$\frac{x^2}{25t}+\frac{y^2}{9t}=1({t>0})$,其中a=$\sqrt{25t}$=5$\sqrt{t}$,b=$\sqrt{9t}$=3$\sqrt{t}$,则有c=$\sqrt{25t-9t}$=4$\sqrt{t}$,
则其长轴长2a=10$\sqrt{t}$,短轴长2b=6$\sqrt{t}$,焦距2c=8$\sqrt{t}$,离心率e=$\frac{c}{a}$=$\frac{4}{5}$;
比较可得,两者的离心率相等;
故选:C.
点评 本题考查椭圆的标准方程,关键是有椭圆的标准方程计算出长轴长、短轴长,焦距、离心率.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
20.设向量$\vec a=({cos{{45}°},sin4{5°}})$,$\vec b=({cos{{15}°},sin{{15}°}})$,$\vec a•\vec b$=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
1.已知函数f(x)=2ex,则( )
| A. | f′(x)=f(x)+2 | B. | f′(x)=f(x) | C. | f′(x)=3f(x) | D. | f′(x)=2f(x) |
18.已知λ∈R,向量$\overrightarrow a=({3,λ})\;,\;\overrightarrow b=({λ-1\;,\;2})$,则“λ=3”是“$\overrightarrow a∥\overrightarrow b$”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
5.命题“若a2+b2=0,则a,b都为零”的否命题是( )
| A. | 若a2+b2≠0,则a,b都不为零 | B. | 若a2+b2≠0,则a,b不都为零 | ||
| C. | 若a,b都不为零,则a2+b2≠0 | D. | 若a,b不都为零,则a2+b2≠0 |
 已知:抛物线m:y2=2px焦点为F,以F为圆心的圆F过原点O,过F引斜率为k的直线与抛物线m和圆F从上至下顺次交于A、B、C、D.若$\overrightarrow{AB}•\overrightarrow{CD}$=4.
已知:抛物线m:y2=2px焦点为F,以F为圆心的圆F过原点O,过F引斜率为k的直线与抛物线m和圆F从上至下顺次交于A、B、C、D.若$\overrightarrow{AB}•\overrightarrow{CD}$=4.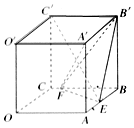 如图,在棱长为2的正方体OABC-O′A′B′C′中,E,F分别是棱AB,BC上的动点.
如图,在棱长为2的正方体OABC-O′A′B′C′中,E,F分别是棱AB,BC上的动点.