题目内容
【题目】已知曲线![]() 上的点到点
上的点到点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小2.
的距离小2.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
, ![]() 两点,若
两点,若![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)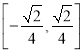
【解析】试题分析:(1)由题意得曲线![]() 是以
是以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线,进而可得其方程为
为准线的抛物线,进而可得其方程为![]() ;(2)设直线
;(2)设直线![]() 为
为![]() ,代入抛物线方程消去
,代入抛物线方程消去![]() 可得
可得![]() ,设
,设![]() ,
, ![]() ,则
,则![]() ,由
,由![]() ,得
,得![]() ,又
,又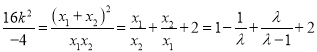 ,可构造
,可构造![]() ,由函数的单调性可得
,由函数的单调性可得![]() ,即
,即![]() ,解得
,解得![]() ,即为所求。
,即为所求。
试题解析:(1)由题意得动点![]() 到
到![]() 的距离等于它到直线
的距离等于它到直线![]() 的距离,
的距离,
∴ 动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线,
为准线的抛物线,
设其方程为![]() ,由条件得
,由条件得![]() .
.
∴ 曲线![]() 的标准方程为
的标准方程为![]() ;
;
(2)由题意设直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
∵ 直线![]() 与抛物线相交,∴
与抛物线相交,∴![]() ,
,
设A(x1,y1),B(x2,y2),则![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() ,
,
由![]() 可得
可得
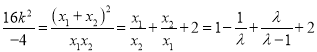 ,
,
即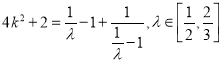 ,
,
∵![]() ,∴
,∴![]() 。
。
设![]() ,则函数
,则函数![]() 在
在![]() 上单调递减。
上单调递减。
∴![]() ,即
,即![]() 。
。
由![]() 得
得![]() ,满足
,满足![]() 。
。
∴![]() 的取值范围为
的取值范围为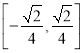 。
。

练习册系列答案
相关题目