Question

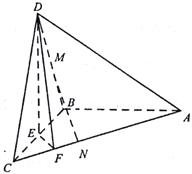
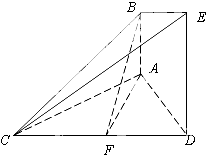
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC

(1)求三棱锥D-ABC的体积

(2)求证:平面DAC⊥平面DEF;

(3)若M为DB中点,N在棱AC上,且CN=CA,求证:MN∥平面DEF

Answer 1

【答案】（1）；（2）见解析；（3）见解析.

【解析】试题分析：（1）根据等积法，利用求解。（2）由题意得，又所以再线面垂直的判定得，从而。又根据题意得到,从而，根据面面垂直的判定可得平面DAC⊥平面DEF。（3）连交于点则得又从而有根据线面平行的判定定理可得MN∥平面DEF。

试题解析：

（1）因为

所以是点到平面的距离，

所以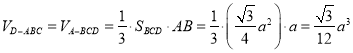

（2）因为是正三角形， 为的中点，

所以

因为

所以

又因为

所以，且,

所以；

因为

所以且

所以,

又因为， ,

所以

因为

所以

（3）连交于点则得

又因为

所以在面

又

所以