题目内容
平面上整点(纵、横坐标都是整数的点)到直线y=
x+
的距离中的最小值是( )
| 5 |
| 3 |
| 4 |
| 5 |
分析:求出平面上点(x,y)到直线的距离为d=
,由于|5(5x-3y+2)+2|≥2,从而求得所求的距离d的最小值.
| |5(5x-3y+2)+2| | ||
5
|
解答:解:直线即25x-15y+12=0,设平面上点(x,y)到直线的距离为d,则 d=
=
.
∵5x-3y+2为整数,故|5(5x-3y+2)+2|≥2,且当x=y=-1时,即可取到2,
故所求的距离的最小值为
=
,
故选B.
| |25x-15y+12| | ||
5
|
| |5(5x-3y+2)+2| | ||
5
|
∵5x-3y+2为整数,故|5(5x-3y+2)+2|≥2,且当x=y=-1时,即可取到2,
故所求的距离的最小值为
| 2 | ||
5
|
| ||
| 85 |
故选B.
点评:本题主要考查点到直线的距离公式的应用,属于基础题.

练习册系列答案
相关题目
 x+
x+ 的距离中的最小值是
的距离中的最小值是


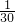
 x+
x+ 的距离中的最小值是( )
的距离中的最小值是( )


