题目内容
16．已知f（x）=log3x．（1）作出这个函数的图象；
（2）若f（a）＜f（2），利用图象求a的取值范围．
分析 （1）因为f（x）=log3x为对数函数，过定点（1，0），结合对数函数的性质，可得函数图象；
（2）由图象可对不等式f（a）＜f（2）直接求解
解答 解：（1）函数y=log3x的图象如图所示：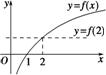
（2）由（1）中函数的图象，可得函数f（x）=log3x的定义域为（0，+∞），
且函数f（x）=log3x为增函数，
若f（a）＜f（2），
则a∈（0，2）
点评 本题考查含有绝对值函数的图象的做法、函数的单调性、解不等式等知识，考查数形结合思想．
练习册系列答案
相关题目
6．某学校高二学生进行研究性学习，某班共有m（m∈N*）名学生编号为1、2、3…m，有n（n∈N*）台设备编号分别为1、2、3…n，定义记号aij；如果第i名学生操作了第j台设备，此时规定aij=1否则aij=0，则等式a41+a42+a43+…a4n=3的实际意义为（ ）
| A． | 第4名学生操作了n台设备 | B． | 第4名学生操作了3台设备 | ||
| C． | 第3名学生操作了n台设备 | D． | 第3名学生操作了4台设备 |
4．
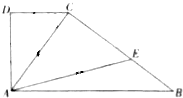如图所示直角梯形ABCD中，∠BAD=∠ADC=90°，∠ACD=60°，AB=3DC=3，若线段BC上存在点E，使得AC、AE、AB成等比数列，则$\frac{CE}{CB}$等于（ ）
如图所示直角梯形ABCD中，∠BAD=∠ADC=90°，∠ACD=60°，AB=3DC=3，若线段BC上存在点E，使得AC、AE、AB成等比数列，则$\frac{CE}{CB}$等于（ ）| A． | $\frac{1+\sqrt{15}}{7}$ | B． | $\frac{6-\sqrt{15}}{7}$ | C． | $\frac{\sqrt{87}-9}{7}$ | D． | $\frac{18-\sqrt{87}}{7}$ |