题目内容
(本小题满分12分)
已知等比数列{an}的各项均为正数,且 2a1 +3a2 =1,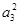 =9a2a6.
=9a2a6.
(Ⅰ) 求数列{an}的通项公式;
(Ⅱ)设 bn=log3a1 +log3a2 +…+ log3an,求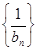 的前n项和Tn;
的前n项和Tn;
(Ⅲ)在(Ⅱ)的条件下,求使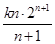 ≥ (7? 2n)Tn恒成立的实数k 的取值范围.
≥ (7? 2n)Tn恒成立的实数k 的取值范围.
已知等比数列{an}的各项均为正数,且 2a1 +3a2 =1,
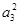 =9a2a6.
=9a2a6.(Ⅰ) 求数列{an}的通项公式;
(Ⅱ)设 bn=log3a1 +log3a2 +…+ log3an,求
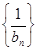 的前n项和Tn;
的前n项和Tn;(Ⅲ)在(Ⅱ)的条件下,求使
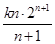 ≥ (7? 2n)Tn恒成立的实数k 的取值范围.
≥ (7? 2n)Tn恒成立的实数k 的取值范围.(Ⅰ) .(Ⅱ)前n 项和为?
.(Ⅱ)前n 项和为? .(Ⅲ)
.(Ⅲ)
 .(Ⅱ)前n 项和为?
.(Ⅱ)前n 项和为? .(Ⅲ)
.(Ⅲ)
试题分析:(1)根据2a1 +3a2 =1,
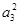 =9a2a6.可建立关于a1和q的方程求出a1和q的值,从而得到{an}的通项公式.
=9a2a6.可建立关于a1和q的方程求出a1和q的值,从而得到{an}的通项公式.(2)再(1)的基础上根据对数的运算性质可得
 ,因而可得
,因而可得 =?2
=?2 ,显然采用叠加求和的方法求和.
,显然采用叠加求和的方法求和.(3)可令
 ,采用作差法求
,采用作差法求 的最大值,从而求出k的范围.
的最大值,从而求出k的范围.(Ⅰ)设数列
 的公比为
的公比为 (q>0),
(q>0),由
 得
得 ,
, .
.故数列
 的通项公式为
的通项公式为 .
.(Ⅱ )bn =log3a1 +log3a2 +…+ log3an =?

故
 =?2
=?2
Tn =
 +
+ +
+ +…+
+…+
= ?2
 =?
=?
所以数列
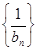 的前n 项和为?
的前n 项和为? .
.(Ⅲ )化简得
 对任意
对任意 恒成立
恒成立设
 ,则
,则
当
 为单调递减数列,
为单调递减数列, 为单调递增数列,
为单调递增数列,所以,n=5时,
 取得最大值为
取得最大值为 .
.所以, 要使
 对任意
对任意 恒成立,
恒成立,
点评:掌握等差等比数列的通项及性质以及常用数列求和的方法是求解此类问题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
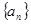 满足
满足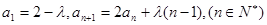
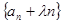 为等比数列;
为等比数列;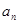 以及前n项和
以及前n项和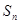 ;
;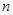 都有
都有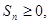 求
求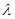 的取值范围。
的取值范围。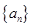 和
和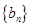 的前
的前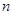 项和分别是
项和分别是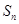 和
和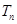 ,已知
,已知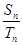 =
=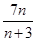 ,则
,则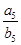 =( )
=( )
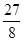
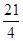
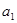 =-2013,
=-2013,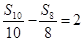 ,则
,则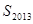 =
=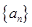 满足
满足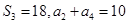 。
。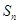 的最大值;
的最大值;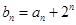 ,求数列
,求数列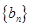 的其前
的其前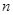 项和
项和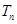 .
.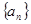 是等差数列,
是等差数列,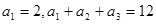
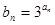 ,求数列
,求数列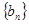 的前n项和Sn.
的前n项和Sn.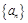 中,若
中,若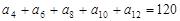 ,则
,则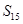 的值为: ( )
的值为: ( )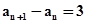 ,则数列
,则数列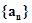 是( )
是( )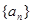 的公差为2,若
的公差为2,若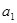 ,
,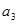 ,
,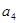 成等比数列,则
成等比数列,则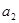 等于( )
等于( )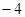 B
B  C
C  D
D