题目内容
如图，以过原点的直线的倾斜角θ为参数，则圆x2＋y2－x＝0的参数方程为________．
(θ为参数)
[解析] 由三角函数定义知
＝tanθ(x≠0)，y＝xtanθ，
由x2＋y2－x＝0得，x2＋x2tan2θ－x＝0，x＝
＝cos2θ，
则y＝xtanθ＝cos2θtanθ＝sinθcosθ，
又θ＝
时，x＝0，y＝0也适合题意，
故参数方程为
(θ为参数)．
[解法探究] 因为直线OP与圆的交点为P，所以点P与直径两端点构成直角三角形，故可通过解直角三角形求得参数方程．
将圆x2＋y2－x＝0配方得，(x－
)2＋y2＝
，
∴圆的直径为1.
设P(x，y)，则|OP|＝cosθ，
x＝|OP|cosθ＝cos2θ，
y＝|OP|sinθ＝sinθcosθ.
∴圆的参数方程为(θ为参数)．
练习册系列答案
相关题目
；
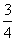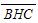的长．
)且与极轴平行的直线的方程是( )
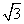B．ρsinθ＝
(t为参数)，C在点(1,1)处的切线为l，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，则l的极坐标方程为________．
)．