题目内容
9.已知P为椭圆$\frac{x^2}{36}+\frac{y^2}{9}=1$上的任意一点,O为坐标原点,M在线段OP上,且$\overrightarrow{OM}=\frac{1}{3}\overrightarrow{OP}$(1)求点M的轨迹E的方程;
(2)若A(-4,0),B(0,4),C为轨迹E上的动点,求△ABC面积的最大值.
分析 (1)设出M,P的坐标,由向量等式把P的坐标用M的坐标表示,代入椭圆方程整理可得点M的轨迹E的方程;
(2)写出直线AB的截距式方程,再设出与直线AB平行的直线l的方程为x-y+m=0,与椭圆方程联立,利用判别式等于0求得m值,结合三角形面积公式得答案.
解答 解:(1)设M(x,y),P(x0,y0),
由$\overrightarrow{OM}=\frac{1}{3}\overrightarrow{OP}$,得$({x,y})=\frac{1}{3}({{x_0},{y_0}})⇒\left\{\begin{array}{l}{x_0}=3x\\{y_0}=3y\end{array}\right.$,
∵P(x0,y0)在椭圆上,
∴$\frac{{{x_0}^2}}{36}+\frac{{{y_0}^2}}{9}=1$,即$\frac{9{x}^{2}}{36}+\frac{9{y}^{2}}{9}=1$,则$\frac{x^2}{4}+{y^2}=1$,
∴点M的轨迹E的方程为$\frac{x^2}{4}+{y^2}=1$;
(2)由题意可得直线AB的方程为x-y+4=0,
设与直线AB平行的直线l的方程为x-y+m=0,
由$\left\{{\begin{array}{l}{x-y+m=0}\\{\frac{x^2}{4}+{y^2}=1}\end{array}}\right.$,得5x2+8mx+4m2-4=0.
令△=0,得64m2-4×5×(4m2-4)=0,解得$m=±\frac{5}{4}$,
∵△ABC的面积$S=\frac{1}{2}\sqrt{{4^2}+{4^2}}\frac{{|{m-4}|}}{{\sqrt{2}}}=2|{m-4}|$,
∴当$m=-\frac{5}{4}$时,△ABC的面积有最大值为$\frac{21}{2}$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,是中档题.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案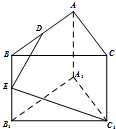 在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )
在正三棱柱ABC-A1B1C1中,AB=2,点D、E分别是棱AB、BB1的中点,若DE⊥EC1,则侧棱AA1的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
| A. | (-∞,0) | B. | (-∞,0] | C. | (-∞,1) | D. | (-∞,1] |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{2}$ |
 椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.
椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),F1,F2分别是它的左、右焦点,已知椭圆C过点(0,1),且离心率e=$\frac{2\sqrt{2}}{3}$.