题目内容
设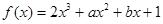 的导数为
的导数为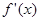 ,若函数
,若函数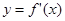 的图象关于直线
的图象关于直线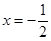 对称,且函数
对称,且函数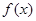 在
在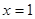 处取得极值.
处取得极值.
(I)求实数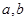 的值;
的值;
(II)求函数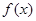 的单调区间.
的单调区间.
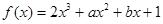 的导数为
的导数为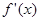 ,若函数
,若函数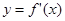 的图象关于直线
的图象关于直线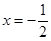 对称,且函数
对称,且函数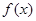 在
在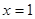 处取得极值.
处取得极值.(I)求实数
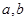 的值;
的值;(II)求函数
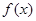 的单调区间.
的单调区间.(I)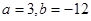 ;(II)函数
;(II)函数 的单调递增区间是
的单调递增区间是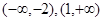 ,单调递减区间是
,单调递减区间是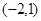 .
.
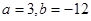 ;(II)函数
;(II)函数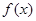 的单调递增区间是
的单调递增区间是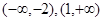 ,单调递减区间是
,单调递减区间是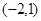 .
.试题分析:(I)求导得:
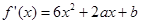 ,这是一个二次函数,其对称轴为
,这是一个二次函数,其对称轴为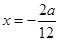 .
.由已知条件可得:
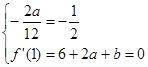 ,解这个方程组,可得
,解这个方程组,可得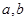 的值.
的值.(II)将
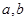 的值代入
的值代入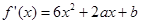 得:
得: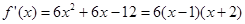 .
.由
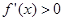 得
得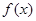 的单调递增区间,由
的单调递增区间,由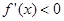 得
得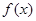 的单调递减区间.
的单调递减区间.试题解析:(I)求导得:
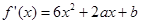 .
.依题意有:
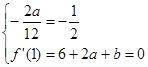 ,解得:
,解得: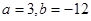 .
.(II)由(I)可得:
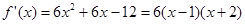 .
.令
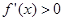 得:
得: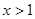 或
或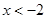 ,
,令
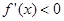 得:
得: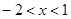 ,
,综上:函数
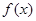 的单调递增区间是
的单调递增区间是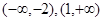 ,单调递减区间是
,单调递减区间是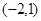 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
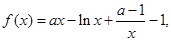 试讨论
试讨论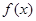 的单调性.
的单调性.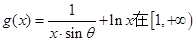 上为增函数,且
上为增函数,且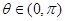 ,
,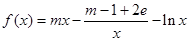 ,
,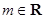 .
.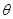 的值;
的值;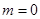 时,求函数
时,求函数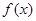 的单调区间和极值;
的单调区间和极值;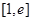 上至少存在一个
上至少存在一个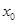 ,使得
,使得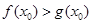 成立,求
成立,求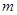 的取值范围.
的取值范围.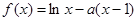 ,
,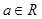 .
.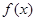 的单调性;
的单调性;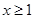 时,
时,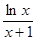 恒成立,求
恒成立,求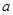 的取值范围.
的取值范围.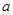 为实数,函数
为实数,函数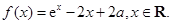
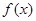 的单调区间与极值;
的单调区间与极值;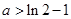 且
且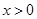 时,
时,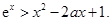
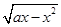 (a>0)的单调递减区间是________.
(a>0)的单调递减区间是________.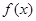 满足:
满足: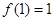 ,且对于任意的
,且对于任意的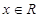 ,都有
,都有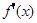 <
<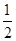 ,则不等式
,则不等式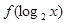 >
>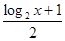 的解集为 .
的解集为 .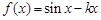 存在极值,则实数
存在极值,则实数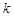 的取值范围是( )
的取值范围是( )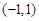
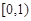
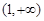
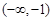
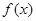 为定义在
为定义在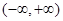 上的可导函数,
上的可导函数,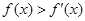 对于
对于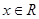 恒成立,且
恒成立,且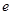 为自然对数的底数,则( )
为自然对数的底数,则( )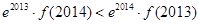
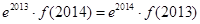
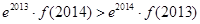
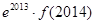 与
与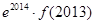 的大小不能确定
的大小不能确定