题目内容
(本小题共14分)
已知椭圆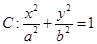
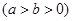 经过点
经过点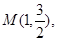 其离心率为
其离心率为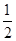 .
.
(Ⅰ)求椭圆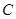 的方程;
的方程;
(Ⅱ)设直线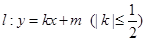 与椭圆
与椭圆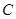 相交于A、B两点,以线段
相交于A、B两点,以线段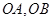 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆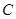 上,
上,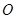 为坐标原点.求
为坐标原点.求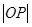 的取值范围.
的取值范围.
【答案】
解:(Ⅰ)由已知可得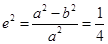 ,所以
,所以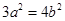 ① ……………1分
① ……………1分
又点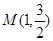 在椭圆
在椭圆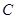 上,所以
上,所以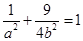 ② ……………2分
② ……………2分
由①②解之,得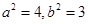 .
.
故椭圆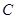 的方程为
的方程为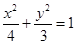 .
……………5分
.
……………5分
(Ⅱ) 当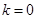 时,
时,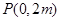 在椭圆
在椭圆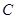 上,解得
上,解得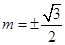 ,所以
,所以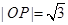 . ……6分
. ……6分
当 时,则由
时,则由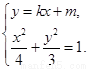
消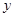 化简整理得:
化简整理得: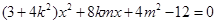 ,
,
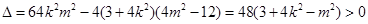 ③
……………8分
③
……………8分
设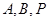 点的坐标分别为
点的坐标分别为 ,则
,则
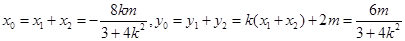 .……9分
.……9分
由于点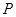 在椭圆
在椭圆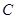 上,所以
上,所以
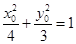 . …………10分
. …………10分
从而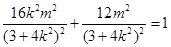 ,化简得
,化简得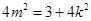 ,经检验满足③式.…11分
,经检验满足③式.…11分
又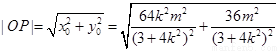
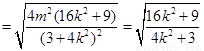
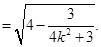 ………………12分
………………12分
因为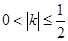 ,得
,得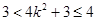 ,有
,有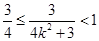 ,
,
故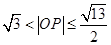 .
………………………13分
.
………………………13分
综上,所求 的取值范围是
的取值范围是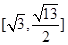 . ………………………14分
. ………………………14分
(Ⅱ)另解:设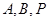 点的坐标分别为
点的坐标分别为 ,
,
由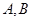 在椭圆上,可得
在椭圆上,可得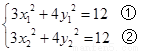 ………………………6分
………………………6分
①—②整理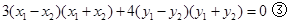 …………………7分
…………………7分
由已知可得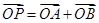 ,所以
,所以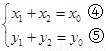 ……………………8分
……………………8分
由已知当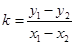 ,即
,即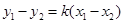 ⑥……………………9分
⑥……………………9分
把④⑤⑥代入③整理得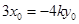 ………………………10分
………………………10分
 所求
所求 的取值范围是
的取值范围是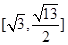 . ………………………14分
. ………………………14分
【解析】略

练习册系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是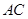 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.