题目内容
如图已知四边形ABCD为直角梯形,SA垂直平面ABCD.SA=AB=BC=1,AD=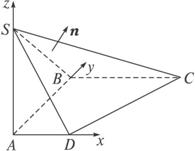
解:令![]() =i,
=i,![]() =j,
=j,![]() =k,以A为坐标原点建立空间直角坐标系A—xyz,则i,j,k为标准正交基底,于是可得
=k,以A为坐标原点建立空间直角坐标系A—xyz,则i,j,k为标准正交基底,于是可得

i=(1,0,0),j=(0,1,0),k=(0,0,1),则D=(![]() ,0,0),S(0,0,1),C(1,1,0),由此可得
,0,0),S(0,0,1),C(1,1,0),由此可得![]() =(
=(![]() ,0,-1),
,0,-1),![]() =(1,1,-1).
=(1,1,-1).
设平面SCD的法向量为n=(x,y,z),则
n·![]() =0,n·
=0,n·![]() =0.
=0.
换用坐标表示,得
(x,y,z)·(![]() ,0,-1)=0,(x,y,z)·(1,1,-1)=0,
,0,-1)=0,(x,y,z)·(1,1,-1)=0,
即
把z作为已知数,解此方程组,得x=2z,y=-z.
令z=1,得n=(2,-1,1).
所以cos〈i,n〉= .
.
设平面 SAB与SCD的夹角为θ,则tanθ=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知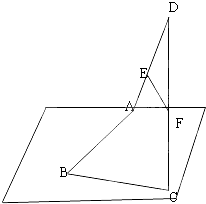 已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.
已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC. 如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
如图,已知四边形ABCD为直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,沿AC将△ABC折起,使点B到点P的位置,且平面PAC⊥平面ACD.
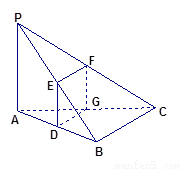 如图,已知三棱锥P—ABC中,PA⊥平面ABC,设AB、PB、PC的中点分别为D、E、F,
如图,已知三棱锥P—ABC中,PA⊥平面ABC,设AB、PB、PC的中点分别为D、E、F,