题目内容
(10)分) 已知正方体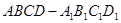 ,
, 是底
是底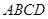 对角线的交点.
对角线的交点.
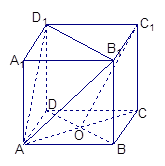
求证:(1)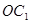 ∥面
∥面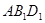 ;(2)
;(2)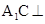 面
面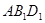 .
.
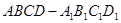 ,
, 是底
是底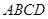 对角线的交点.
对角线的交点.
求证:(1)
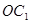 ∥面
∥面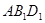 ;(2)
;(2)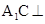 面
面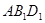 .
. 见解析。
本题主要考查了线面平行、线面垂直的判定定理,考查对基础知识的综合应用能力和基本定理的掌握能力.
(1)欲证C1O∥面AB1D1,根据直线与平面平行的判定定理可知只需证C1O与面AB1D1内一直线平行,连接A1C1,设A1C1∩B1D1=O1,连接AO1,易得C1O∥AO1,AO1?面AB1D1,C1O?面AB1D1,满足定理所需条件;
(2)欲证A1C⊥面AB1D1,根据直线与平面垂直的判定定理可知只需证A1C与面AB1D1内两相交直线垂直根据线面垂直的性质可知A1C⊥B1D1,同理可证A1C⊥AB1,又D1B1∩AB1=B1,满足定理所需条件.
证明:(1)连结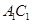 ,设
,设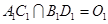 连结
连结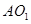 ,
,
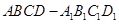 是正方体
是正方体
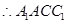 是平行四边形
是平行四边形
∴A1C1∥AC且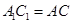
又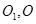 分别是
分别是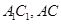 的中点,
的中点,
∴O1C1∥AO且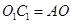
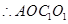 是平行四边形
是平行四边形
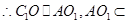 面
面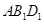 ,
,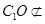 面
面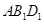
∴C1O∥面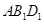
(2)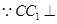 面
面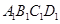
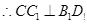
又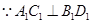 ,
, 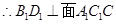
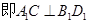
同理可证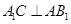 ,
,
又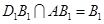
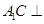 面
面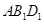
(1)欲证C1O∥面AB1D1,根据直线与平面平行的判定定理可知只需证C1O与面AB1D1内一直线平行,连接A1C1,设A1C1∩B1D1=O1,连接AO1,易得C1O∥AO1,AO1?面AB1D1,C1O?面AB1D1,满足定理所需条件;
(2)欲证A1C⊥面AB1D1,根据直线与平面垂直的判定定理可知只需证A1C与面AB1D1内两相交直线垂直根据线面垂直的性质可知A1C⊥B1D1,同理可证A1C⊥AB1,又D1B1∩AB1=B1,满足定理所需条件.
证明:(1)连结
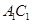 ,设
,设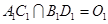 连结
连结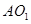 ,
,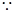
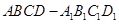 是正方体
是正方体 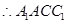 是平行四边形
是平行四边形∴A1C1∥AC且
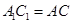
又
 分别是
分别是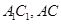 的中点,
的中点,∴O1C1∥AO且
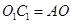
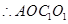 是平行四边形
是平行四边形 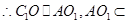 面
面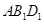 ,
,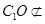 面
面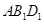
∴C1O∥面
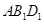
(2)
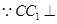 面
面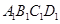
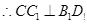
又
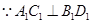 ,
, 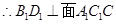
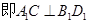
同理可证
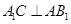 ,
, 又
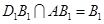
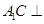 面
面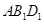

练习册系列答案
相关题目
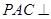 平面
平面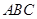 ,
,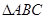 是以
是以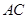 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,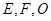 分别为
分别为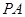 ,
,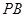 ,
,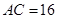 ,
,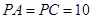 .
.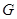 是
是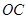 的中点,证明:
的中点,证明: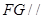 平面
平面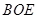 ;
;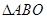 内是否存在一点
内是否存在一点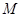 ,使
,使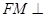 平面
平面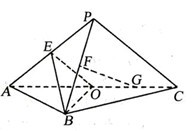
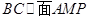 ;(Ⅱ)求证:平面MAP⊥平面SAC;
;(Ⅱ)求证:平面MAP⊥平面SAC;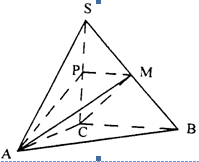
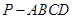 中,
中, 底面
底面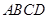 ,四边形
,四边形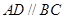 ,
,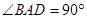 ,
, ,
,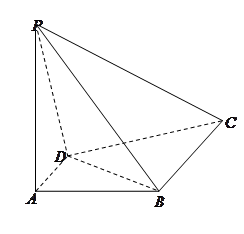
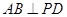 ;
;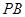 上找出一点
上找出一点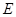 ,使
,使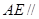 平面
平面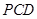 ,
, 面ABC,BC
面ABC,BC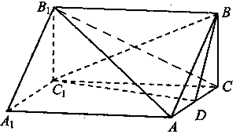
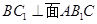 ;
;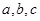 是三条直线,若
是三条直线,若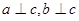 ,则
,则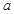 ∥
∥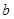 ”,得出如下结论:
”,得出如下结论: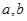 是两条直线,
是两条直线,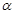 是平面,若
是平面,若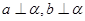 ,则
,则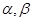 是两个平面,
是两个平面,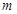 是直线,若
是直线,若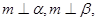 则
则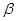 ;
;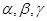 是三个平面,若
是三个平面,若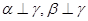 ,则
,则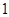
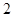
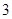
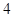
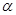 和直线l,则
和直线l,则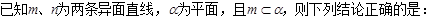 ( )
( )