题目内容
14.二次函数f(x)=ax2-$\sqrt{2}$bx+c,其中a,b,c是某钝角三角形的三边,且三边中b最长.(1)试证明函数有两个零点;
(2)若a=c,试求零点α,β间距离|α-β|的取值范围.
分析 (1)证明方程有两个不等实根,即只要验证△>0即可.
(2)根据二次方程根与系数的关系,将|α-β|转化为某变量的函数,再求它的变化范围.
解答 (本小题满分12分)
解:(1)在钝角△ABC中,b边最长.
$则{b^2}>{a^2}+{c^2},△={(-\sqrt{2}b)^2}-4ac=2{b^2}-4ac>2({a^2}+{c^2})-4ac=2{(a-c)^2}≥0$,
∴函数有两个零点.
(2)零点为α,β.又a=c,
∴${|{α-β}|^2}={({α+β})^2}-4αβ=\frac{{2{b^2}}}{a^2}-4$=$\frac{{2({a^2}+{c^2}-2accosB)-4{a^2}}}{a^2}=-4cosB$,
∵-1<cosB<0,
∴0<-4cosB<4,
∴0<|α-β|<2.
点评 本题是以一元二次方程作为,考查解三角形的有关定理,余弦定理作为研究三角形边角关系的一大工具,应用广泛.通过余弦定理沟通了三角函数与三角形有关性质,在研究较复杂的三角形问题时,常需正、余弦定理联袂出场、密切协作,方能解决问题,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.已知△ABC中,A=90°,AB=3,AC=2.已知λ∈R,且点P,Q满足$\overrightarrow{AP}$=λ$\overrightarrow{AB}$,$\overrightarrow{AQ}$=(1-λ)$\overrightarrow{AC}$,若$\overrightarrow{BQ}$•$\overrightarrow{CP}$=-6,则λ=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{5}$ |
6.已知为虚数单位,复数z满足z=$\frac{1+i}{1-i}$,则z2=( )
| A. | 1 | B. | -1 | C. | 2i | D. | -2i |
3.袋中装有5个同样大小的球,编号为1,2,3,4,5.现从该袋内随机取出3个球,记被取出的球的最大号码数为ξ,则Eξ等于( )
| A. | 4 | B. | 4.5 | C. | 4.75 | D. | 5 |
4.设等比数列{an}的通项为an=$\frac{1}{n(n+1)}$,则其前10项的和S10等于( )
| A. | $\frac{9}{10}$ | B. | $\frac{11}{10}$ | C. | $\frac{10}{9}$ | D. | $\frac{10}{11}$ |
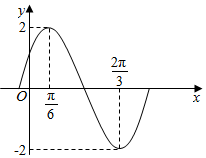 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)(x∈R)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)(x∈R)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;