题目内容
(本小题满分12分)
已知函数 。
。
(1)求 的振幅和最小正周期;
的振幅和最小正周期;
(2)求当 时,函数
时,函数 的值域;
的值域;
(3)当 时,求
时,求 的单调递减区间。
的单调递减区间。
(1)振幅2,最小正周期为 ;(2)
;(2)
(3)
解析试题分析:(1)第一问利用三角函数的解析式得到其振幅,结合周期公式得到结论。
(2)先求解原函数的递减区间,然后根据集合的交集的运算得到给定区间的递减区间。
(1)
所以,振幅2,最小正周期为
(2)
(3)

所以
考点:本题主要是考查三角函数的图形与性质的运用。
点评:解决该试题的关键是理解振幅的概念和周期公式的运用以及结正弦函数的单调区间来求解给定区间的递减区间。

练习册系列答案
相关题目
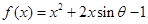 ,
,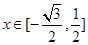
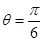 时,求
时,求 的最大值和最小值
的最大值和最小值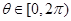 ,求
,求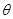 的取值范围
的取值范围
 的最小正周期; 2)求函数
的最小正周期; 2)求函数 上的对称轴方程与零点.
上的对称轴方程与零点.

 的最小正周期、单调增区间、对称轴和对称中心;
的最小正周期、单调增区间、对称轴和对称中心; 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
 的最小正周期为
的最小正周期为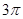 ,当
,当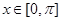 时,函数
时,函数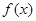 的最小值为0。
的最小值为0。 ,若
,若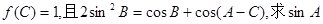 的值。
的值。 终边上一点
终边上一点 的坐标为
的坐标为 ,
, ;
; 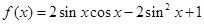
 的最小正周期和值域 (2)求
的最小正周期和值域 (2)求 ,(
,( )
) 的最小正周期和单调递增区间;
的最小正周期和单调递增区间; 时,求
时,求