题目内容
11.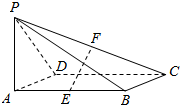 如图,已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD=1,AB=$\sqrt{2}$,点E,F分别为AB、PC中点.
如图,已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD=1,AB=$\sqrt{2}$,点E,F分别为AB、PC中点.(1)求证:EF⊥PD;
(2)求点E到平面PDC的距离.
分析 (1)取PD的中点M,可得AEFM为平行四边形,AM∥EF,根据AM⊥PD,证得EF⊥PD.
(2)设点E到平面PDC的距离为h,由于AE平行于平面PCD,故点E到平面PDC的距离等于点A到平面PDC的距离,再根据由VP-ACD=VE-PCD,求得h的值.
解答  解:(1)如图所示:已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,取PD的中点M,
解:(1)如图所示:已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,取PD的中点M,
∵E为AB的中点,
故AE∥MF,AE=MF,∴AEFM为平行四边形,∴AM∥EF.
由PA=AD=1,AB=$\sqrt{2}$,可得PAD为等腰直角三角形,AM⊥PD,故EF⊥PD.
(2)由于PCD PCE都是直角三角形,利用勾股定理求得PC=2,PD=$\sqrt{2}$,
设点E到平面PDC的距离为h.
由于AE平行于平面PCD,故点E到平面PDC的距离等于点A到平面PDC的距离.
由VP-ACD=VE-PCD 可得 $\frac{1}{3}$•S△ACD•PA=$\frac{1}{3}$•S△PCD•h,
可得•S△ACD•PA=S△PCD•h,即$\frac{1}{2}$•AD•CD•PA=$\frac{1}{2}$•PD•CD•h,即AD•PA=PD•h,
即1×1=$\sqrt{2}$•h,求得 h=$\frac{\sqrt{2}}{2}$ 点E到平面PDC的距离为$\frac{\sqrt{2}}{2}$.
点评 本题主要考查证明直线和直线垂直的方法,用等体积法求点到平面的距离,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
1.空间四边形ABCD的各边及对角线均相等,E是边BC的中点,那么( )
| A. | $\overrightarrow{AE}•\overrightarrow{BC}$<$\overrightarrow{AE}•\overrightarrow{CD}$ | B. | $\overrightarrow{AE}•\overrightarrow{BC}$=$\overrightarrow{AE}•\overrightarrow{CD}$ | ||
| C. | $\overrightarrow{AE}•\overrightarrow{BC}$>$\overrightarrow{AE}•\overrightarrow{CD}$ | D. | $\overrightarrow{AE}•\overrightarrow{BC}$与$\overrightarrow{AE}•\overrightarrow{CD}$不能比较大小 |
18.圆的方程为x2+y2+2by-2b2=0,则圆的圆心和半径分别为( )
| A. | (0,b),$\sqrt{3}$b | B. | (0,b),$\sqrt{3}$|b| | C. | (0,-b),$\sqrt{3}$b | D. | (0,-b),$\sqrt{3}$|b| |
3.已知x,y满足约束条件$\left\{{\begin{array}{l}{x-y≥0}\\{x+y≤2}\\{y≥0}\end{array}}\right.$,则z=2x+y的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.已知实数x,y满足$\left\{\begin{array}{l}{x+y-1≥0}\\{x-y≤0}\\{x≥0}\end{array}\right.$,则2x-y的最大值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 0 |