题目内容
1．已知实数x，y满足$\left\{\begin{array}{l}{x+y-1≥0}\\{x-y≤0}\\{x≥0}\end{array}\right.$，则2x-y的最大值为（ ）| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 0 |
分析 作出平面区域，变形目标函数z=2x-y平移直线y=2x可得结论．
解答 解：作出$\left\{\begin{array}{l}{x+y-1≥0}\\{x-y≤0}\\{x≥0}\end{array}\right.$所对应的区域（如图阴影），
变形目标函数z=2x-y可得y=2x-z，平移直线y=2x可得：
当直线经过点A（$\frac{1}{2}$，$\frac{1}{2}$）时，直线的截距最小，z取最大值，
代值计算可得zmax=2×$\frac{1}{2}$-$\frac{1}{2}$=$\frac{1}{2}$
故选：B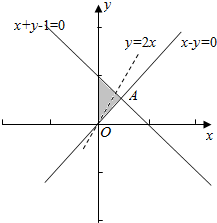
点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
11．
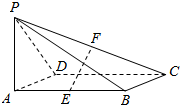如图，已知四棱锥P-ABCD的底面为矩形，PA⊥底面ABCD，且PA=AD=1，AB=$\sqrt{2}$，点E，F分别为AB、PC中点．
（1）求证：EF⊥PD；
（2）求点E到平面PDC的距离．
如图，已知四棱锥P-ABCD的底面为矩形，PA⊥底面ABCD，且PA=AD=1，AB=$\sqrt{2}$，点E，F分别为AB、PC中点．（1）求证：EF⊥PD；
（2）求点E到平面PDC的距离．
12．若函数f（x）=$\left\{\begin{array}{l}{1，（x∈Q）}\\{0，（x∈{∁}_{R}Q）}\end{array}\right.$，则f（e）=（ ）（其中e是自然对数的底数）
| A． | 0 | B． | 1 | C． | 0或1 | D． | 不确定 |
16．已知f（x）满足f（x+2）=f（x）和f（-x）=-f（x），且当x∈（0，1）时，f（x）=3x-1，则f（$\frac{2015}{2}$）=（ ）
| A． | $\sqrt{3}+1$ | B． | $\sqrt{3}-1$ | C． | -$\sqrt{3}-1$ | D． | -$\sqrt{3}+$ |
10．
已知定义在R上的函数f（x）的图象如图，则x•f′（x）＞0的解集为（ ）
已知定义在R上的函数f（x）的图象如图，则x•f′（x）＞0的解集为（ ）| A． | （-∞，0）∪（1，2） | B． | （1，2） | C． | （-∞，1） | D． | （-∞，1）∪（2，+∞） |