题目内容
3.已知△ABC的两边AC=1,AB=2,∠A的平分线与BC边交于点D,AD=1,求△ABC的面积.(提示:下面结论可以直接应用无需证明.结论:在△ABC中,∠A的平分线与BC边交于点D,则有$\frac{AB}{AC}$=$\frac{BD}{DC}$).分析 由AD为角平分线,利用角平分线性质列出比例式,找出BD与CD关系,设BD=2x,DC=x,利用余弦定理表示出cos∠ADB与-cos∠ADC,代入cos∠ADB=-cos∠ADC,求出x的值,确定出cos∠BAC的值,进而求出sin∠BAC的值,利用三角形面积公式即可求出三角形ABC面积.
解答 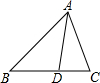 解:∵AD为∠BAC的平分线,
解:∵AD为∠BAC的平分线,
∴$\frac{AB}{AC}$=$\frac{BD}{CD}$=2,
设BD=2x,DC=x,
∵cos∠ADB=-cos∠ADC=$\frac{1+4{x}^{2}-4}{4x}$=-$\frac{1+{x}^{2}-1}{2x}$,
整理得:x=$\frac{\sqrt{2}}{2}$(负值舍去),
∴cos∠BAC=$\frac{1+4-9{x}^{2}}{4}$=$\frac{1}{8}$,
∴sin∠BAC=$\sqrt{1-co{s}^{2}∠BAC}$=$\frac{3\sqrt{7}}{8}$,
则S△ABC=$\frac{1}{2}$×1×2sinA=$\frac{3\sqrt{7}}{8}$.
点评 此题考查了余弦定理,三角形面积公式,以及同角三角函数间的基本关系,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列四个命题中真命题的是( )
| A. | 经过定点p(x0,y0)的直线都可能用方程y-y0=k(x-x0)表示 | |
| B. | 经过任意两个不同的点p1(x1,y1),p2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示 | |
| C. | 经过定点A(0,b)的直线都可以用方程y=kx+b表示 | |
| D. | 不经过原点的直线都可以用方程$\frac{x}{a}$+$\frac{y}{b}$=1表示 |
18.已知实数a,b满足如下两个条件:(1)关于x的方程3x2-2x-ab=0有两个异号的实根;(2)$\frac{2}{a}$+$\frac{1}{b}$=1,若对于上述的一切实数a,b,不等式a+2b>m2+2m恒成立,则实数m的取值范围是( )
| A. | (-4,2) | B. | (-2,4) | C. | (-∞,-4]∪[2,+∞) | D. | (-∞,-2]∪[4,+∞) |
8.在△ABC中,若2bccosBcosC=b2sin2C+c2sin2B,那么△ABC是( )
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
15.已知数列{an}满足an+1=qan+2q-2(q为常数,|q|<1),若a3,a4,a5,a6∈{-18,-6,-2,6,30},则a1=( )
| A. | -2 | B. | -2或126 | C. | 128 | D. | 0或128 |
12.函数f(x)=xe-x在[0,4]上的最小值为( )
| A. | $\frac{4}{e^4}$ | B. | $\frac{1}{e}$ | C. | 0 | D. | $\frac{2}{e^2}$ |