题目内容
△ABC为一个等腰三角形形状的空地,腰AC的长为3(百米),底AB的长为4(百米).现决定在空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为S1和S2.
(1)若小路一端E为AC的中点,求此时小路的长度;
(2)若小路的端点E、F两点分别在两腰上,求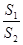 的最小值.
的最小值.
(1)  百米 (2)
百米 (2) 
解析解:(1)∵E为AC中点时,
则AE=EC= ,
,
∵ +3<
+3< +4,
+4,
∴F不在BC上.
故F在AB上,
可得AF= ,
,
在三角形ABC中,cosA= .
.
在三角形AEF中,EF2=AE2+AF2-2AE·AFcosA= ,
,
∴EF= .
.
即小路一端E为AC中点时小路的长度为 百米.
百米.
(2)若小路的端点E、F两点分别在两腰上,如图所示,
设CE=x,CF=y,
则x+y=5,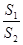 =
= =
= -1
-1
= -1=
-1= -1≥
-1≥ -1
-1
= ,
,
当x=y= 时取等号.
时取等号.
答:最小值为 .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 .
.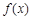 的最小正周期和值域;
的最小正周期和值域;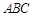 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 且
且 ,
,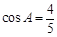 ,求
,求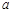 和
和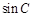 .
. )的值.
)的值.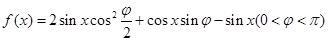 在
在 处取最小值.
处取最小值. 的值。
的值。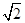 ,
,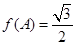 ,求角C.
,求角C. .
. -cos 2A的值.
-cos 2A的值. ,求bc的最大值.
,求bc的最大值.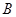 为钝角的
为钝角的 的内角
的内角 的对边分别为
的对边分别为 、
、 、
、 ,
, ,且
,且 与
与 垂直。
垂直。 的取值范围.
的取值范围.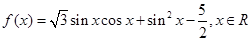 .
.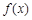 最大值和最小正周期;
最大值和最小正周期;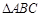 内角
内角 所对的边分别为
所对的边分别为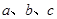 ,且
,且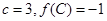 .若
.若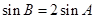 ,求
,求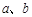 的值.
的值. )海里的两个观测点,现位于A点北偏东45°、B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
)海里的两个观测点,现位于A点北偏东45°、B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距20
 c=b.
c=b. c-2b=1,求角B.
c-2b=1,求角B.