题目内容
已知函数 ,且定义域为(0,2).
,且定义域为(0,2).
(1)求关于x的方程 +3在(0,2)上的解;
+3在(0,2)上的解;
(2)若 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数 的取值范围;
的取值范围;
(3)若关于x的方程 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解 ,求k的取值范围。
,求k的取值范围。
 ,且定义域为(0,2).
,且定义域为(0,2).(1)求关于x的方程
 +3在(0,2)上的解;
+3在(0,2)上的解;(2)若
 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数 的取值范围;
的取值范围;(3)若关于x的方程
 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解 ,求k的取值范围。
,求k的取值范围。(1) ,
, +3即
+3即
当 时,
时, ,此时该方程无解………………1分
,此时该方程无解………………1分
当 时,
时, ,原方程等价于:
,原方程等价于: 此时该方程的解为
此时该方程的解为 .
.
综上可知:方程 +3在(0,2)上的解为
+3在(0,2)上的解为 . ………………3分
. ………………3分
(2)
 ,
,
 ………………4分
………………4分
 , ……………… 5分
, ……………… 5分
可得:若 是单调递增函数,则
是单调递增函数,则
 ………………6分
………………6分
若 是单调递减函数,则
是单调递减函数,则
 ,……………… 7分
,……………… 7分
综上可知: 是单调函数时
是单调函数时 的取值范围为
的取值范围为 .………8分
.………8分
(2)[解法一]:当 时,
时, ,①
,①
当 时,
时, ,②
,②
若k=0则①无解,②的解为 故
故 不合题意 ……………9分
不合题意 ……………9分
若 则①的解为
则①的解为 ,
,
(Ⅰ)当 时,
时, 时,方程②中
时,方程②中
故方程②中一根在(1,2)内另一根不在(1,2)内, ……………… 10分
设 ,而
,而 则
则 又
又 ,
,
故 ,
,

 ,
, +3即
+3即
当
 时,
时, ,此时该方程无解………………1分
,此时该方程无解………………1分当
 时,
时, ,原方程等价于:
,原方程等价于: 此时该方程的解为
此时该方程的解为 .
.综上可知:方程
 +3在(0,2)上的解为
+3在(0,2)上的解为 . ………………3分
. ………………3分(2)

 ,
, ………………4分
………………4分  , ……………… 5分
, ……………… 5分可得:若
 是单调递增函数,则
是单调递增函数,则
 ………………6分
………………6分 若
 是单调递减函数,则
是单调递减函数,则
 ,……………… 7分
,……………… 7分综上可知:
 是单调函数时
是单调函数时 的取值范围为
的取值范围为 .………8分
.………8分(2)[解法一]:当
 时,
时, ,①
,①当
 时,
时, ,②
,②若k=0则①无解,②的解为
 故
故 不合题意 ……………9分
不合题意 ……………9分若
 则①的解为
则①的解为 ,
,(Ⅰ)当
 时,
时, 时,方程②中
时,方程②中
故方程②中一根在(1,2)内另一根不在(1,2)内, ……………… 10分
设
 ,而
,而 则
则 又
又 ,
,故
 ,
, 
略

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 的函数
的函数 满足
满足 .
. ,求
,求 ;又若
;又若 ,求
,求 ;
; ,使得
,使得 ,求函数
,求函数 ,
, 是二次函数,当
是二次函数,当 时,
时, ,且
,且 为奇函数,求函数
为奇函数,求函数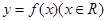 满足
满足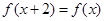 且
且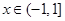 时
时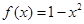 ,函数
,函数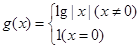 ,则函数
,则函数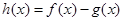 在区间
在区间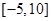 内零点的个数为( )
内零点的个数为( ) 在定义域内零点的个数是( )
在定义域内零点的个数是( )  、
、 、
、
 ,且
,且 ,
, ,
, ,则
,则 的值( )
的值( )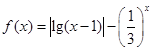 有两个零点x1,x2,则有
有两个零点x1,x2,则有



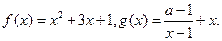
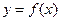 和
和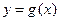 的公共点个数;
的公共点个数;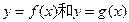 的公共点个数恰为两个。
的公共点个数恰为两个。 满足
满足
 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围; (
(