题目内容
【题目】已知函数![]() 在区间
在区间![]() 上的最大值为2.
上的最大值为2.
(1)求函数![]() 的解析式,并求它的对称中心的坐标;
的解析式,并求它的对称中心的坐标;
(2)先将函数![]() 保持横坐标不变,纵坐标变为原来的
保持横坐标不变,纵坐标变为原来的![]() (
(![]() )倍,再将图象向左平移
)倍,再将图象向左平移![]() (
(![]() )个单位,得到的函数
)个单位,得到的函数![]() 为偶函数.若对任意的
为偶函数.若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]()
![]() ;(2)
;(2)![]()
【解析】
(1)化简![]() ,
,![]() 时,
时, ![]() 取最大值
取最大值![]() ,即有
,即有![]() ,得
,得![]() ,再求出对称中心坐标;
,再求出对称中心坐标;
(2)求出![]() 解析式,
解析式,![]() ,只需
,只需![]() 的值域是
的值域是![]() 值域的子集即可.
值域的子集即可.
(1)![]() .
.
∵![]() ,∴
,∴![]() ,
,
则当![]() ,即
,即![]() 时,
时, ![]() 取最大值
取最大值![]() ,即有
,即有![]() ,得
,得![]() .
.
∴![]() ;
;
令![]() ,解得
,解得![]()
![]() ,
,
∴![]() 的对称中心的坐标为
的对称中心的坐标为![]()
![]() .
.
(2)![]() ,
,
∵![]() 为偶函数,∴
为偶函数,∴![]()
![]() ,∴
,∴![]()
![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() 的值域为
的值域为![]() ;
;
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
①当![]() 时,
时,![]() 的值域为
的值域为![]() ,
,
②当![]() 时,
时,![]() 的值域为
的值域为![]() ,
,
而依据题意有![]() 的值域是
的值域是![]() 值域的子集,
值域的子集,
则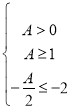 或
或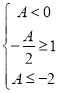
∴![]() 或
或![]() ,所以实数
,所以实数![]() 的取值范围为
的取值范围为![]()

练习册系列答案
相关题目
【题目】为了解本届高二学生对文理科的选择与性别是否有关,现随机从高二的全体学生中抽取了若干名学生,据统计,男生35人,理科生40人,理科男生30人,文科女生15人。
(1)完成如下2×2列联表,判断是否有99.9%的把握认为本届高二学生“对文理科的选择与性别有关”?
男生 | 女生 | 合计 | |
文科 | |||
理科 | |||
合计 |
(2)已采用分层抽样的方式从样本的所有女生中抽取了5人,现从这5人中随机抽取2人参加座谈会,求抽到的2人恰好一文一理的概率。
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式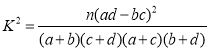 ,其中
,其中![]() 为样本容量)
为样本容量)



