题目内容
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() 到抛物线
到抛物线![]() 焦点的距离为
焦点的距离为![]() .
.
(1)求![]() 的值;
的值;
(2) 设![]() 是抛物线上异于
是抛物线上异于![]() 的两个不同点,过
的两个不同点,过![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,过
,过![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 分别交于点
分别交于点![]() .
.
求证:①直线![]() 的斜率为定值;
的斜率为定值;
②![]() 是线段
是线段![]() 的中点.
的中点.

【答案】(1) ![]() ,
,![]() ..
..
(2) ①证明见解析. ②证明见解析.
【解析】分析:(1)由抛物线定义知,![]() 所以
所以![]() ,将点
,将点![]() 代入抛物线得
代入抛物线得![]() ,
,![]() ;(2) 设
;(2) 设![]() 求得
求得![]() ,
,![]() ,利用斜率公式消去
,利用斜率公式消去![]() 、
、![]() 可得直线
可得直线![]() 的斜率为
的斜率为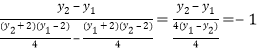 ;②设点
;②设点![]() 的横坐标分别为
的横坐标分别为![]() ,求得
,求得![]() ,
,![]() ,根据中点坐标公式化简即可的结果.
,根据中点坐标公式化简即可的结果.
详解:(1)由抛物线定义知,![]()
所以![]() ,
,
将点![]() 代入抛物线得
代入抛物线得![]() ,
,![]()
(2)设![]()
①则直线![]() 的方程为:
的方程为: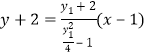
令![]() 得,
得,![]() ,所以
,所以![]()
同理![]()
所以直线![]() 的斜率为
的斜率为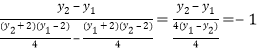 (定值)
(定值)
②设点![]() 的横坐标分别为
的横坐标分别为![]()
由①知,直线![]() 的方程为:
的方程为:![]()
令![]() 得,
得,![]()
又直线![]() 的方程为:
的方程为:![]()
令![]() 得,
得,![]()
所以![]()
![]()
![]()
![]()
所以![]() 是线段
是线段![]() 的中点.
的中点.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目



