题目内容
若直线mx-ny+1=0(m>0,n>0)和函数f(x)=ax+1+1(a>0且a≠1)的图象恒过同一个定点,则
+
的最小值为
| 2 |
| m |
| 1 |
| n |
8
8
.分析:利用基本不等式的性质和“乘1法”即可得出.
解答:解:f(x)=ax+1+1过定点(-1,2),又点在直线上,
∴m+2n=1,
∴(
+
)(m+2n)=4+
+
≥4+2
=8(当且仅当m=2n=
时取等号).
故答案为8.
∴m+2n=1,
∴(
| 2 |
| m |
| 1 |
| n |
| 4n |
| m |
| m |
| n |
| 4 |
| 1 |
| 2 |
故答案为8.
点评:熟练掌握本不等式的性质和“乘1法”是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
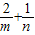 的最小值为 .
的最小值为 .