题目内容
已知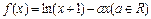
(1)当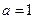 时,求
时,求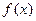 在定义域上的最大值;
在定义域上的最大值;
(2)已知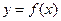 在
在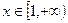 上恒有
上恒有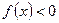 ,求
,求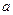 的取值范围;
的取值范围;
(3)求证: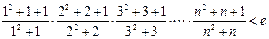
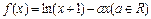
(1)当
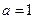 时,求
时,求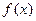 在定义域上的最大值;
在定义域上的最大值;(2)已知
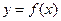 在
在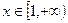 上恒有
上恒有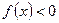 ,求
,求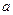 的取值范围;
的取值范围;(3)求证:
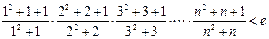
(1) ,所以
,所以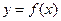 在
在 为增,在
为增,在 为减,所以
为减,所以 时,
时, 取最大值
取最大值 。
。
(2)等价 恒成立,设
恒成立,设 ,
,
设 ,
,
所以 是减函数,所以
是减函数,所以 ,
,
所以 是减函数,
是减函数, ,所以
,所以
(也可用构造函数 利用数形结合解答)
利用数形结合解答)
(3)要证 ,
,
只证
只证
因为 ,
,
所以
 ,所以
,所以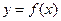 在
在 为增,在
为增,在 为减,所以
为减,所以 时,
时, 取最大值
取最大值 。
。(2)等价
 恒成立,设
恒成立,设 ,
,设
 ,
,所以
 是减函数,所以
是减函数,所以 ,
,所以
 是减函数,
是减函数, ,所以
,所以
(也可用构造函数
 利用数形结合解答)
利用数形结合解答)(3)要证
 ,
,只证

只证

因为
 ,
,所以

略

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
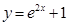 在点
在点 处的切线与直线
处的切线与直线 和
和 围成的三角形的面积为
围成的三角形的面积为



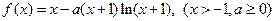 .
.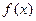 的单调区间;
的单调区间;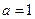 时,若方程
时,若方程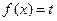 在
在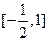 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;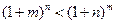 .
.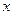 +
+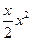 (
(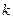 ≥0)。
≥0)。 在
在 轴上的截距为1,且曲线上一点
轴上的截距为1,且曲线上一点 处的切线斜率为
处的切线斜率为 .(1)曲线在P点处的切线方程;(2)求函数
.(1)曲线在P点处的切线方程;(2)求函数 的极大值和极小值
的极大值和极小值 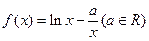 。
。 在定义域上的单调性;
在定义域上的单调性;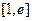 上的最小值为2,求
上的最小值为2,求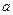 的值。
的值。 上一点
上一点 ,则在点
,则在点 处的切线的倾斜角为
处的切线的倾斜角为



 的导数是( )
的导数是( )




 ,若满足
,若满足 ,则必有( )
,则必有( )


