题目内容
设函数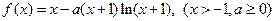 .
.
(1)求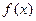 的单调区间;
的单调区间;
(2)当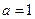 时,若方程
时,若方程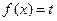 在
在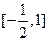 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(3)证明:当m>n>0时,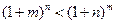 .
.
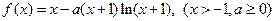 .
.(1)求
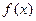 的单调区间;
的单调区间;(2)当
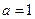 时,若方程
时,若方程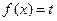 在
在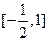 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;(3)证明:当m>n>0时,
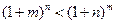 .
.22、(Ⅰ)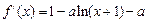
①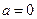 时,
时,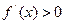 ∴
∴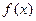 在(—1,+
在(—1,+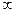 )上市增函数
)上市增函数
②当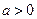 时,
时,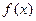 在
在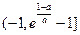 上递增,在
上递增,在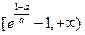 单调递减
单调递减
(Ⅱ)由(Ⅰ)知,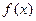 在
在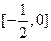 上单调递增,在
上单调递增,在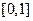 上单调递减
上单调递减
又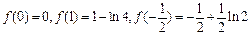 ∴
∴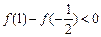
∴当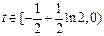 时,方程
时,方程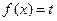 有两解
有两解
(Ⅲ)要证: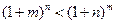 只需证
只需证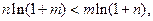
只需证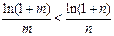
设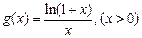 , 则
, 则
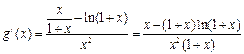
由(Ⅰ)知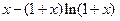 在
在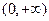 单调递减
单调递减
∴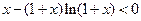 ,即
,即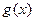 是减函数,而m>n
是减函数,而m>n
∴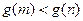 ,故原不等式成立
,故原不等式成立
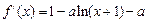
①
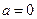 时,
时,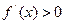 ∴
∴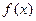 在(—1,+
在(—1,+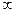 )上市增函数
)上市增函数②当
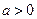 时,
时,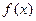 在
在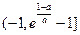 上递增,在
上递增,在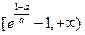 单调递减
单调递减(Ⅱ)由(Ⅰ)知,
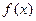 在
在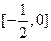 上单调递增,在
上单调递增,在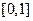 上单调递减
上单调递减又
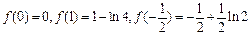 ∴
∴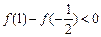
∴当
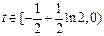 时,方程
时,方程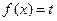 有两解
有两解(Ⅲ)要证:
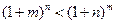 只需证
只需证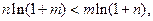
只需证
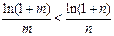
设
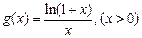 , 则
, 则
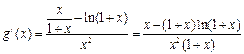
由(Ⅰ)知
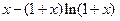 在
在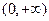 单调递减
单调递减∴
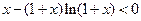 ,即
,即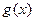 是减函数,而m>n
是减函数,而m>n∴
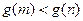 ,故原不等式成立
,故原不等式成立略

练习册系列答案
相关题目
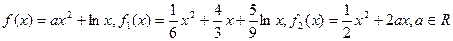 .
.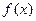 在点
在点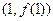 处的切线恒过定点,并求出定点坐标;
处的切线恒过定点,并求出定点坐标;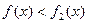 在区间
在区间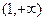 上恒成立,求
上恒成立,求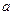 的取值范围;
的取值范围;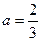 时,求证:在区间
时,求证:在区间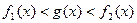 恒成立的函数
恒成立的函数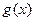
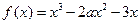 ,
,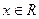 .
.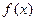 在
在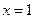 处取得极值,求
处取得极值,求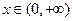 时,
时,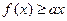 恒成立,求
恒成立,求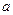 的取值范围.
的取值范围.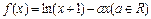
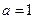 时,求
时,求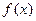 在定义域上的最大值;
在定义域上的最大值;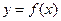 在
在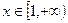 上恒有
上恒有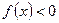 ,求
,求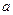 的取值范围;
的取值范围;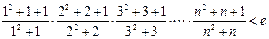
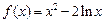 .
.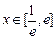 时,不等式
时,不等式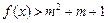 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;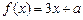 在区间[
在区间[ 1,3]上恰好有两个相异的实根,求实数
1,3]上恰好有两个相异的实根,求实数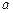 的取值范围.
的取值范围.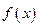 为定义在R上的偶函数,且导数
为定义在R上的偶函数,且导数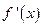 存在,则
存在,则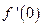 的值为 ( ▲ )
的值为 ( ▲ )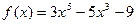 的极值点的个数( ▲ )
的极值点的个数( ▲ ) 在点
在点 处的切线方程为( )
处的切线方程为( )



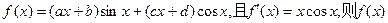 = 。
= 。