题目内容
已知函数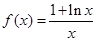 .
.
(1)若函数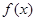 在区间
在区间 上有极值,求实数
上有极值,求实数 的取值范围;
的取值范围;
(2)若关于 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围;
的取值范围;
(3)当 ,
, 时,求证:
时,求证: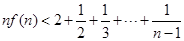 .
.
(1)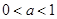
(2)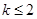
(3)根据数列的求和来放缩法得到不等式的证明关键是对于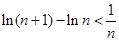 的运用。
的运用。
解析试题分析:解:(1)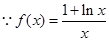 ,
,
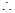 当
当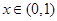 时,
时,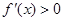 ;当
;当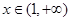 时,
时, ;
; 函数
函数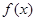 在区间(0,1)上为增函数;在区间
在区间(0,1)上为增函数;在区间 为减函数 3分
为减函数 3分 当
当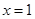 时,函数
时,函数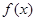 取得极大值,而函数
取得极大值,而函数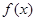 在区间
在区间 有极值.
有极值.
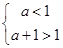 ,解得
,解得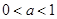 . 5分
. 5分
(2)由(1)得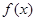 的极大值为
的极大值为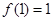 ,令
,令 ,所以当
,所以当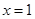 时,函数
时,函数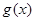 取得最小值
取得最小值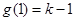 ,又因为方程
,又因为方程 有实数解,那么
有实数解,那么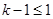 ,即
,即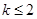 ,所以实数
,所以实数 的取值范围是:
的取值范围是: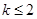 . 10分
. 10分
(另解: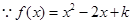 ,
,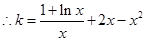 ,
,
令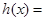
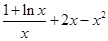 ,所以
,所以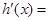
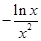
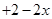 ,当
,当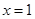 时,
时,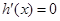
当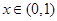 时,
时,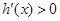 ;当
;当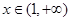 时,
时,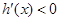
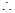 当
当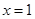 时,函数
时,函数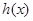 取得极大值为
取得极大值为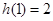
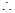 当方程
当方程 有实数解时,
有实数解时,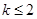 .)
.)
(3)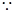 函数
函数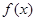 在区间
在区间 为减函数,而
为减函数,而 ,
,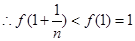
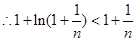 ,即
,即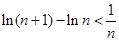
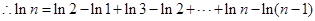
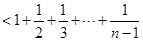 12分
12分
即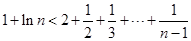 ,
,
而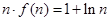 ,
, 结论成立. 16分
结论成立. 16分
考点:导数的运用
点评:根据导数的符号判定函数的单调性,是解决该试题的关键,同时能结合函数与方程的思想求解方程的根,属于中档题。

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 为
为
 阶“期待数列”:
阶“期待数列”: ;②
;②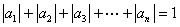 .
. 为
为 (
(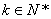 )阶“期待数列”,求公比
)阶“期待数列”,求公比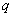 ;
;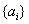 的前
的前 项和为
项和为 :
: ;
; 使
使 ,试问数列
,试问数列 能否为
能否为 ,
, 为正整数.
为正整数. 和
和 的值;
的值; 的通项公式为
的通项公式为 (
( ),求数列
),求数列 ;
; 满足:
满足: ,
, ,设
,设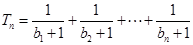 ,若(Ⅱ)中的
,若(Ⅱ)中的 恒成立,试求m的最大值.
恒成立,试求m的最大值. 都是等差数列,且公差相等,(1)求
都是等差数列,且公差相等,(1)求 的通项公式;(2)若
的通项公式;(2)若 的前三项,记数列
的前三项,记数列 数列
数列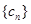 的前n项和为
的前n项和为
 的前
的前 项和
项和 ,数列
,数列 满足
满足
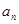 ;(2)求数列
;(2)求数列 ;
; 恒成立
恒成立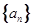 中,
中,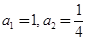 ,且
,且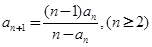 .
.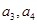 ,猜想
,猜想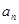 的表达式,并加以证明;
的表达式,并加以证明;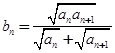 ,求证:对任意的自然数
,求证:对任意的自然数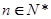 ,都有
,都有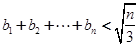 ;
; 的前n项和
的前n项和 (n为正整数)。
(n为正整数)。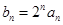 ,求证数列
,求证数列 是等差数列,并求数列
是等差数列,并求数列 ,
, 试比较
试比较 与
与 的大小,并予以证明。
的大小,并予以证明。 共有
共有 项(整数
项(整数 ),首项
),首项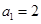 ,设该数列的前
,设该数列的前 项和为
项和为 ,且
,且 其中常数
其中常数 ⑴求
⑴求 ,数列
,数列 满足
满足
 ;
; ,求
,求 的最大值.
的最大值.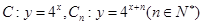 ,从
,从 上的点
上的点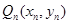 作
作 轴的垂线,交
轴的垂线,交 于点
于点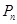 ,再从点
,再从点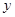 轴的垂线,交
轴的垂线,交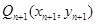 ,
,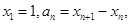
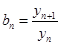 .。
.。 求数列
求数列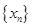 的通项公式;
的通项公式;  记
记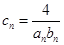 ,数列
,数列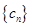 的前
的前 项和为
项和为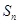 ,试比较
,试比较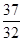 的大小
的大小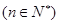 ;
;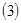 记
记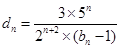 ,数列
,数列 的前
的前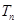 ,试证明:
,试证明: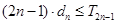 。
。