题目内容
如图,长方体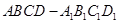 中,
中,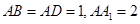 ,点
,点 为
为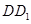 的中点.
的中点.
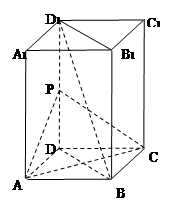
(1)求证:直线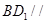 平面
平面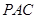 ;
;
(2)求证:平面 平面
平面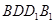 ;
;
(3)求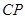 与平面
与平面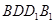 所成的角大小.
所成的角大小.
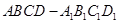 中,
中,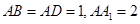 ,点
,点 为
为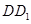 的中点.
的中点.
(1)求证:直线
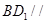 平面
平面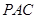 ;
;(2)求证:平面
 平面
平面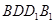 ;
;(3)求
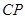 与平面
与平面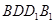 所成的角大小.
所成的角大小.(1)见解析;(2)见解析;(3) .
.
 .
.试题分析:(1)记
 ,先作辅助线
,先作辅助线 ,这几乎是用几何法证明线面平行、线面垂直的必经之路了,对些考生要有意识,然后根据线面平行的判定定理进行证明即可;(2)要证明平面
,这几乎是用几何法证明线面平行、线面垂直的必经之路了,对些考生要有意识,然后根据线面平行的判定定理进行证明即可;(2)要证明平面 平面
平面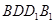 ,只须证
,只须证 平面
平面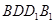 ,然后又只须证明平面
,然后又只须证明平面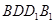 的两条相交直线
的两条相交直线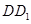 、
、 与
与 垂直;从而实现平面
垂直;从而实现平面 平面
平面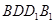 ;(3)由(2)可知,只须求出
;(3)由(2)可知,只须求出 ,在直角三角形
,在直角三角形 进行求解即可.
进行求解即可.试题解析:证明:(1)设
 和
和 交于点
交于点 ,连
,连
由
 分别是
分别是 ,
, 的中点,故
的中点,故
∵
 平面
平面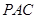 ,
, 平面
平面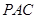
所以直线
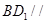 平面
平面
(2)长方体
 中,
中, ,底面
,底面 是正方形,则
是正方形,则
,又
 面
面 ,则
,则

 ,
,∵
 平面
平面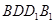 ,
, 平面
平面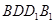 ,
,
∴

 面
面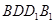
∵
 平面
平面
∴平面

 平面
平面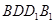
(3)由(2)已证:

 面
面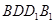
∴
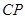 在平面
在平面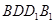 内的射影为
内的射影为
∴
 是
是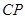 与平面
与平面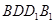 所成的角
所成的角依题意得
 ,
,
在
 中,
中, ,∴
,∴
∴
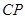 与平面
与平面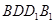 所成的角为
所成的角为 .
.
练习册系列答案
相关题目
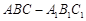 中,
中,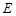 ,
,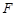 分别为
分别为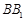 ,
,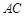 的中点.
的中点.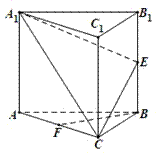
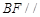 平面
平面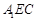 ;
;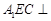 平面
平面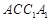 .
.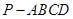 中,底面
中,底面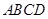 为菱形,
为菱形,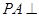 平面
平面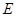 为
为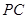 的中点,
的中点,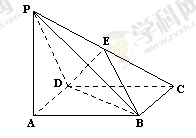
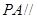 平面
平面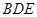 ; (II)平面
; (II)平面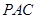 ⊥平面
⊥平面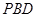 .
.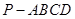 中,底面四边形
中,底面四边形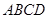 是菱形,
是菱形,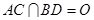 ,
,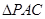 是边长为2的等边三角形,
是边长为2的等边三角形,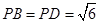 ,
,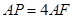 .
.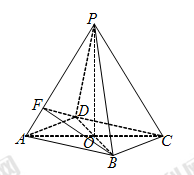
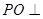 底面
底面 与平面
与平面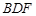 所成角的大小;
所成角的大小;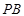 上是否存在一点
上是否存在一点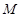 ,使得
,使得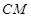 ∥平面
∥平面 ?如果存在,求
?如果存在,求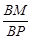 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.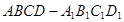 中,
中,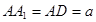 ,
,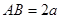 , E、
, E、 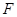 分别为
分别为 、
、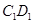 的中点.
的中点.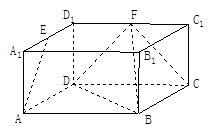
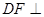 平面
平面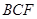 ;
;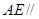 平面
平面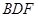 .
.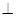 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN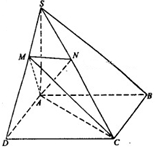
 ,平面
,平面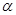 .则“
.则“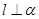 ”是“
”是“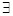 直线
直线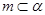 ,
,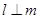 ”的( )
”的( )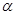 、
、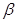 是两个不重合的平面,m、m是两条不重合的直线,则以下结论错误的是
是两个不重合的平面,m、m是两条不重合的直线,则以下结论错误的是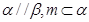 ,则
,则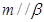
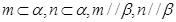 ,则
,则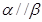
 ,则
,则
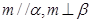 ,则
,则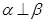
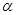 不垂直平面
不垂直平面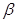 ,那么平面
,那么平面 不平行平面
不平行平面