题目内容
函数 在区间
在区间 上递减,则实数
上递减,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.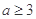 |
B
解析试题分析:本试题是二次函数中区间定轴动的问题,先求出函数的对称轴,再确定出区间与对称轴的位置关系求出实数a的取值范围。由题意,函数的对称轴是x=1-a
∵函数f(x)=x2+ax+3在区间(-∞,2]上递减,则只要满足区间在对称轴的的左侧即可,那么必有, 1-a≥4,解得a≤-3,故答案为:a≤-3,选B.
考点:本题主要考查了函数单调性的性质.
点评:解答本题的关键是熟练掌握了二次函数的性质与图象,根据其性质与图象直接得出关于参数的不等式,求出其范围

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. 和 和 | D. |
函数 的图像与
的图像与 轴的交点个数为 ( )
轴的交点个数为 ( )
| A.一个 | B.至少一个 | C.至多两个 | D.至多一个 |
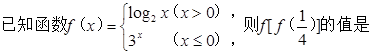 ( )
( )
A. | B.9 | C. | D.-9 |
定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则( )
A.f(sin )<f(cos )<f(cos ) ) | B.f(sin1)>f(cos1) |
C.f(cos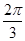 )<f(sin )<f(sin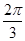 ) ) | D.f(cos2)>f(sin2) |
方程 的根的个数是( )
的根的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
f(x)= ,则f{f[f(-3)]}等于
,则f{f[f(-3)]}等于
| A.0 | B.π | C.π2 | D.9 |
定义在R上的任意函数f (x)都可以表示成一个奇函数g (x)和一个偶函数h (x)之和,如果f (x)=lg(10x+1),x∈R.那么
| A.g (x)=x,h (x)=lg(10x+10-x+1) |
B.g (x)= ,h (x)= ,h (x)= |
C.g (x)= ,h (x)=lg(10x+1)- ,h (x)=lg(10x+1)- |
D.g (x)=- ,h (x)= ,h (x)= |
设 ,则 ( )
,则 ( )
| A.y3>y1>y2 | B.y2>y1>y3 | C.y1>y2>y3 | D.y1>y3>y2 |