题目内容
函数
的图像恒过定点
，若点在直线
上，其中
，则
的最小值为（ ）
| A．1 | B．2 | C．3 | D．4 |
B
解析试题分析：函数的图像恒过定点，所以点的坐标为
，又因为点在直线上，所以
又因为，所以
，
所以
，当且仅当
时等号成立.
考点：本小题主要考查对数函数图象过定点问题和基本不等式的应用，考查学生的转化能力和运算求解能力.
点评：利用基本不等式时，要注意“一正二定三相等”三个条件缺一不可，而且题目中所用的“1”的整体代换是一种常用的解题的技巧.
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
相关题目
已知定义在R上的奇函数
，满足
,且在区间[0,2]上是减函数,则（ ）
A． | B． |
C． | D． |
（ ）
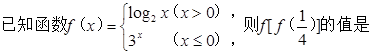A． | B．9 | C． | D．－9 |
方程
的根的个数是（ ）
| A．0个 | B．1个 | C．2个 | D．3个 |
f(x)＝
，则f{f［f(－3)］}等于
| A．0 | B．π | C．π2 | D．9 |
已知函数
的值域是
，则实数
的取值范围是（ ）
A． | B． | C． | D． |
定义在R上的任意函数f (x)都可以表示成一个奇函数g (x)和一个偶函数h (x)之和，如果f (x)＝lg(10x＋1)，x∈R．那么
| A．g (x)＝x，h (x)＝lg(10x＋10－x＋1) |
B．g (x)＝ ，h (x)＝ |
C．g (x)＝ ，h (x)＝lg(10x＋1)－ |
| D．g (x)＝－，h (x)＝ |
函数
的图象必经过点（ ）
| A．（0，1） | B．（1，1） | C．（2，1） | D．（2，2） |
已知
，函数
的图象只可能是（ ）
A． | B． |
C． | D． |