题目内容
2.已知实数x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ 2x-y-2≤0\end{array}\right.$z=x+y,则满足z≥1的点(x,y)所构成的区域面积等于( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
分析 由约束条件作出可行域,画出目标函数z=x+y取最小值1的直线,然后求三角形面积得答案.
解答 解:由约束条件$\left\{\begin{array}{l}y≤x\\ 2x-y-2≤0\end{array}\right.$作出可行域如图,
作出直线x+y=0,平移直线x+y=0至过A(1,0)时,满足目标函数z=x+y有最小值为1,
则满足z≥1的点(x,y)所构成的区域为图中阴影区域.
联立$\left\{\begin{array}{l}{y=x}\\{2x-y-2=0}\end{array}\right.$,解得B(2,2),
联立$\left\{\begin{array}{l}{y=x}\\{x+y=1}\end{array}\right.$,解得C($\frac{1}{2},\frac{1}{2}$),
∴|AC|=$\sqrt{(1-\frac{1}{2})^{2}+(0-\frac{1}{2})^{2}}=\frac{\sqrt{2}}{2}$.
点B到x+y=1的距离为$\frac{|1×2+1×2-1|}{\sqrt{2}}=\frac{3\sqrt{2}}{2}$.
∴${S}_{△ABC}=\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{3\sqrt{2}}{2}=\frac{3}{4}$.
故选:C.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
10.已知椭圆C1与双曲线C2有相同的左右焦点F1、F2,P为椭圆C1与双曲线C2在第一象限内的一个公共点,设椭圆C1与双曲线C2的离心率为e1,e2,且$\frac{{e}_{1}}{{e}_{2}}$=$\frac{1}{3}$,若∠F1PF2=$\frac{π}{3}$,则双曲线C2的渐近线方程为( )
| A. | x±y=0 | B. | x±$\frac{\sqrt{3}}{3}$y=0 | C. | x±$\frac{\sqrt{2}}{2}$y=0 | D. | x±2y=0 |
17.已知(3+2i)x=2-yi,其中 x,y是实数,则|x+yi|=( )
| A. | 2 | B. | $\frac{{2\sqrt{5}}}{3}$ | C. | $\frac{{\sqrt{10}}}{3}$ | D. | $\frac{1}{3}$ |
14.已知函数f(x)=2x+sinx,不等式f(m2)+f(2m-3)<0(其中m∈R)的解集是( )
| A. | (-3,1) | B. | (-1,3) | C. | (-∞,-3)∪(1,+∞) | D. | (-∞,-1)∪(3,+∞) |
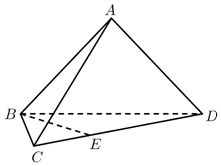 如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC.
如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,点E在CD上,DE=2EC. 在△ABC中,D、E分别是AB、AC的中点,M是直线DE上的动点.若△ABC的面积为2,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为2$\sqrt{3}$.
在△ABC中,D、E分别是AB、AC的中点,M是直线DE上的动点.若△ABC的面积为2,则$\overrightarrow{MB}$•$\overrightarrow{MC}$+$\overrightarrow{BC}$2的最小值为2$\sqrt{3}$.