题目内容
△ABC中，AB=AC=5，BC=6，PA=8且PA⊥平面ABC，则P到BC的距离为
- A.
- B.
- C.
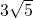
- D.
D
分析：由P是等腰三角形ABC所在平面外一点，PA⊥平面ABC，我们易得PB=PC，取BC的中点D，则AD⊥BC，且PD⊥BC，利用勾股定理我们易求出AD的长，进而求出PD的长，即点P到BC的距离．
解答：
解：如下图所示：
设D为等腰三角形ABC底面上的中点，则PD长即为P点到BC的距离
又∵AD即为三角形的中线，也是三角形BC边上的高
∵BC=6，AB=AC=5，易得AD=4
在直角三角形PAD中，又∵PA=8
∴PD=4
故选D
点评：本题考查的知识点是空间点、线、面之间的距离，其中利用三角形的性质，做出PD即为点P到BC的垂线段是解答本题的关键．
分析：由P是等腰三角形ABC所在平面外一点，PA⊥平面ABC，我们易得PB=PC，取BC的中点D，则AD⊥BC，且PD⊥BC，利用勾股定理我们易求出AD的长，进而求出PD的长，即点P到BC的距离．
解答：
解：如下图所示：设D为等腰三角形ABC底面上的中点，则PD长即为P点到BC的距离
又∵AD即为三角形的中线，也是三角形BC边上的高
∵BC=6，AB=AC=5，易得AD=4
在直角三角形PAD中，又∵PA=8
∴PD=4
故选D
点评：本题考查的知识点是空间点、线、面之间的距离，其中利用三角形的性质，做出PD即为点P到BC的垂线段是解答本题的关键．
练习册系列答案
相关题目
在△ABC中，
=
，
=
，且
=2
，则
等于（ ）
| AB |
| a |
| AC |
| b |
| BD |
| DC |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
在△ABC中，
=a，
=b，D是BC的中点，则
等于（ ）
| AB |
| AC |
| AD |
A、a-
| ||||
B、
| ||||
C、
| ||||
D、-
|