题目内容
若cosα=
,α∈(-
,0),则tanα=( )
| 1 |
| 3 |
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、--2
| ||||
D、2
|
分析:利用同角三角函数的基本关系,由cosα及α的范围求出sinα,从而求出tanα.
解答:解:∵cosα=
,α∈(-
,0),∴sinα=-
=-
,
∴tanα=
=-2
,
故选 C.
| 1 |
| 3 |
| π |
| 2 |
| 1-cos2α |
2
| ||
| 3 |
∴tanα=
| sinα |
| cosα |
| 2 |
故选 C.
点评:本题考查同角三角函数的基本关系的应用,以及三角函数在各个象限中的符号,求出sinα值是解题的关键,注意sinα 的符号.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
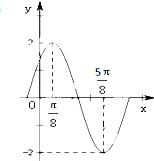 已知函数f(x)=Asin(ωx+φ)(其中A>0,
已知函数f(x)=Asin(ωx+φ)(其中A>0,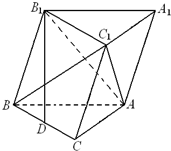 已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成角为θ,点B1在底面上的射影D落在BC上.
已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,侧棱与底面所成角为θ,点B1在底面上的射影D落在BC上.