题目内容
已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，0＜φ＜| π |
| 2 |
（1）求A，ω及?的值；
（2）若cosα=
| 1 |
| 3 |
| π |
| 8 |
分析：（1）根据函数的最大值，得A=2，由函数的周期得ω=2，再由f(
)=2得sin（
+φ）=1，结合0＜φ＜
得ω=
；
（2）结合（1）的结论，得到函数的表达式为f（x）=2sin（2x+
），从而f(α+
)=2cos2α，再用二倍角的余弦公式，可算出f(α+
)的值．
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
（2）结合（1）的结论，得到函数的表达式为f（x）=2sin（2x+
| π |
| 4 |
| π |
| 8 |
| π |
| 8 |
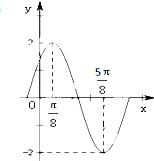
解答：解：（1）由图知函数的最大值为2，所以A=2，…（2分）
∵函数周期T=2（
-
）=π，…（3分）
∴
=2，解之得，…（4分）
∴f（x）=2sin（2x+φ）
又∵f(
)=2sin（
+φ）=2，∴sin（
+φ）=1，…（5分）
∴
+φ=
+2kπ，φ=
+2kπ，（k∈Z）
∵0＜φ＜
，∴φ=
…（7分）
（2）由（1）知：f（x）=2sin（2x+
） …（9分）
∴f(α+
)=2sin（2α+
）=2cos2α …（10分）
∵cosα=
，
∴2cos2α=4cos2α-2=4×(
)2-2=-
…（14分）
∵函数周期T=2（
| 5π |
| 8 |
| π |
| 8 |
∴
| 2π |
| ω |
∴f（x）=2sin（2x+φ）
又∵f(
| π |
| 8 |
| π |
| 4 |
| π |
| 4 |
∴
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
∵0＜φ＜
| π |
| 2 |
| π |
| 4 |
（2）由（1）知：f（x）=2sin（2x+
| π |
| 4 |
∴f(α+
| π |
| 8 |
| π |
| 2 |
∵cosα=
| 1 |
| 3 |
∴2cos2α=4cos2α-2=4×(
| 1 |
| 3 |
| 14 |
| 9 |
点评：本题给出函数y=Asin（ωx+φ）的部分图象，要求确定其解析式．着重考查了三角函数的图象与性质、三角函数的恒等变换及化简求值等知识，属于基础题．
练习册系列答案
相关题目