Question

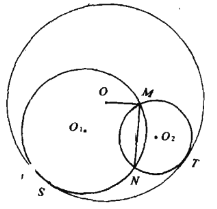
【题目】如图，已知两个半径不相等的与相交于M、N两点，且、分别与内切于S、T两点。求证：OM⊥MN的充分必要条件是S、N、T三点共线。

Answer 1

【答案】见解析

【解析】

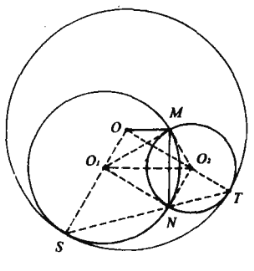
如图，设的半径分别为.由条件知三点共线，三点共线，且OS=OT=r.连结.

充分性.设S、N、T三点共线，则∠S=∠T.又与均为等腰三角形.

故∠S=∠,∠T=∠.

于是，∠S≈∠，∠T=∠.

从而，.

故四边形为平行四边形.

因此，，

.

故.

从而，.由此得.

又由于，故.

必要性.若，，有.从而..

设OM=a，由，，知与的周长都等于，记.

由三角形面积的海伦公式，有.

化简得.

又已知，有.

故，.

所以，为平行四边形.从而，.

又与均为等腰三角形，，，即，.于是，.

故 ,.

所以,S、N、T三点共线.