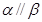题目内容
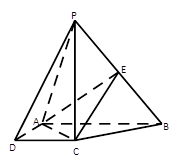
如图,在四棱锥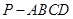 中,
中,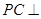 底面
底面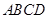 ,
,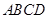 是直角梯形,
是直角梯形,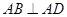 ,
,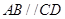 ,
,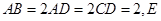 是
是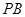 的中点。
的中点。
(1)求证:平面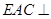 平面
平面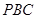 (4分)
(4分)
(2)若二面角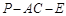 的余弦值为
的余弦值为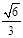 ,求直线
,求直线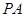 与平面
与平面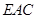 所成角的正弦值.(8分)
所成角的正弦值.(8分)
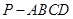 中,
中,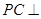 底面
底面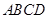 ,
,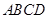 是直角梯形,
是直角梯形,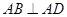 ,
,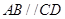 ,
,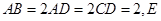 是
是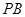 的中点。
的中点。
(1)求证:平面
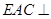 平面
平面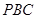 (4分)
(4分)(2)若二面角
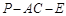 的余弦值为
的余弦值为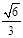 ,求直线
,求直线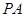 与平面
与平面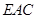 所成角的正弦值.(8分)
所成角的正弦值.(8分)(Ⅰ)见解析(Ⅱ)直线PA与平面EAC所成角的正弦值为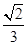 .
.
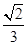 .
.(1)先由线线垂直证明线面垂直,然后再证明面面垂直;(2)建立空间直角坐标系,然后利用直线的方向向量与平面的法向量的夹角与线面角互余求解
(Ⅰ)∵PC⊥平面ABCD,ACÌ平面ABCD,∴AC⊥PC,∵AB=2,AD=CD=2,∴AC=BC=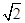 ,
,
∴AC2+BC2=AB2,∴AC⊥BC,又BC∩PC=C,∴AC⊥平面PBC,∵ACÌ平面EAC,∴平面EAC⊥平面PBC.
(Ⅱ)如图,以C为原点,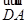 、
、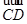 、
、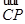 分别为x轴、y轴、z轴正向,建立空间直角坐标系,则C(0,0,0),A(1,1,0),B(1,-1,0).设P(0,0,a)(a>0),
分别为x轴、y轴、z轴正向,建立空间直角坐标系,则C(0,0,0),A(1,1,0),B(1,-1,0).设P(0,0,a)(a>0),

则E(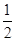 ,-
,-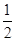 ,
,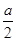 ),
), 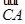 =(1,1,0),
=(1,1,0),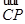 =(0,0,a),
=(0,0,a),
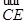 =(
=(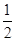 ,-
,-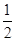 ,
,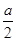 ),取m=(1,-1,0),则m·
),取m=(1,-1,0),则m·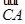 =m·
=m·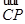 =0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·
=0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·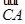 =n·
=n·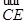 =0,
=0,
即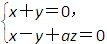 取x=a,y=-a,z=-2,则n=(a,-a,-2),
取x=a,y=-a,z=-2,则n=(a,-a,-2),
依题意,|cosám,nñ|=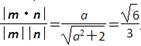 ,则a=2.…10分
,则a=2.…10分
于是n=(2,-2,-2),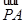 =(1,1,-2).
=(1,1,-2).
设直线PA与平面EAC所成角为θ,则sinθ=|cosá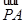 ,nñ|=
,nñ|=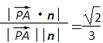 ,
,
即直线PA与平面EAC所成角的正弦值为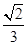
(Ⅰ)∵PC⊥平面ABCD,ACÌ平面ABCD,∴AC⊥PC,∵AB=2,AD=CD=2,∴AC=BC=
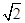 ,
,∴AC2+BC2=AB2,∴AC⊥BC,又BC∩PC=C,∴AC⊥平面PBC,∵ACÌ平面EAC,∴平面EAC⊥平面PBC.
(Ⅱ)如图,以C为原点,
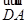 、
、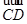 、
、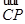 分别为x轴、y轴、z轴正向,建立空间直角坐标系,则C(0,0,0),A(1,1,0),B(1,-1,0).设P(0,0,a)(a>0),
分别为x轴、y轴、z轴正向,建立空间直角坐标系,则C(0,0,0),A(1,1,0),B(1,-1,0).设P(0,0,a)(a>0),
则E(
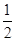 ,-
,-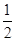 ,
,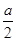 ),
), 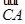 =(1,1,0),
=(1,1,0),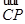 =(0,0,a),
=(0,0,a),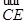 =(
=(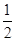 ,-
,-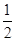 ,
,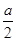 ),取m=(1,-1,0),则m·
),取m=(1,-1,0),则m·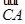 =m·
=m·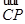 =0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·
=0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·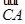 =n·
=n·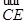 =0,
=0,即
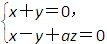 取x=a,y=-a,z=-2,则n=(a,-a,-2),
取x=a,y=-a,z=-2,则n=(a,-a,-2),依题意,|cosám,nñ|=
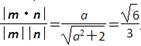 ,则a=2.…10分
,则a=2.…10分于是n=(2,-2,-2),
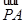 =(1,1,-2).
=(1,1,-2).设直线PA与平面EAC所成角为θ,则sinθ=|cosá
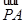 ,nñ|=
,nñ|=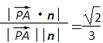 ,
,即直线PA与平面EAC所成角的正弦值为
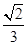

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ∥平面
∥平面 ;
;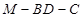 的余弦值。
的余弦值。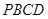 ,
,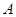 为
为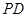 上一点,且
上一点,且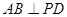 ,
,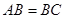 ,
,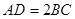 ,沿着
,沿着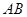 折叠使得二面角
折叠使得二面角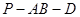 为
为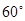 的二面角,连结
的二面角,连结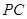 、
、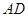 上取一点
上取一点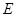 使得
使得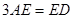 ,连结
,连结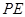 得到如下图(图2)的一个几何体.
得到如下图(图2)的一个几何体.
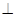 平面
平面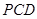 ;
;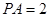 ,求点
,求点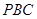 的距离.
的距离.
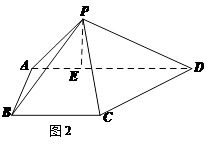
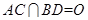 ,
,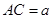 ,得到三棱锥
,得到三棱锥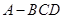 ,如图所示。
,如图所示。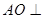 平面BCD;
平面BCD;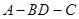 的大小为
的大小为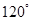 时,
时,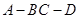 的正切值。
的正切值。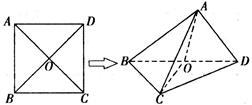
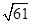
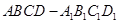 中,
中,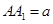 ,
,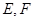 分别是
分别是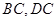 的中点,则异面直线
的中点,则异面直线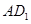 与
与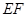 所成角为
所成角为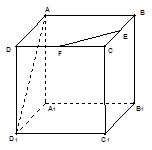
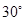
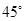
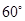
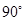
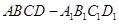 .则下列四个命题
.则下列四个命题
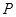 在直线
在直线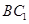 上运动时,三棱锥
上运动时,三棱锥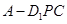 的体积不变;
的体积不变;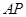 与平面
与平面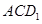 所成的角的大小不变;
所成的角的大小不变;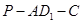 的大小不变;
的大小不变; 是平面
是平面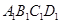 上到点
上到点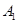 和
和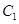 距离相等的点,则
距离相等的点,则
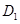 ;
;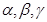 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题: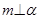 ,
,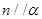 ,则
,则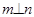 ②若
②若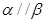 ,
,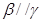 ,
,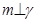
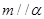 ,
,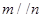 ④若
④若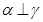 ,
,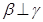 ,则
,则