题目内容
设数列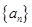 的前
的前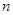 项和为
项和为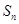 .已知
.已知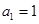 ,
,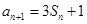 ,
,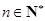 .
.
(Ⅰ)求数列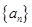 的通项公式;(Ⅱ)记
的通项公式;(Ⅱ)记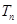 为数列
为数列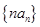 的前
的前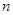 项和,求
项和,求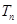 .
.
(Ⅰ) (Ⅱ)
(Ⅱ)
解析试题分析:(Ⅰ)由题意,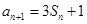 ,则当
,则当 时,
时, .
.
两式相减,得 (
( ).
).
又因为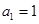 ,
, ,
, ,
,
所以数列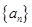 是以首项为
是以首项为 ,公比为
,公比为 的等比数列,
的等比数列,
所以数列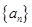 的通项公式是
的通项公式是 (
(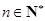 ).
).
(Ⅱ)因为 ,
,
所以 ,
,
两式相减得, ,
,
整理得, (
(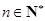 ).
).
考点:数列递推式
点评:本题考查数列的通项与求和,考查错位相减法,考查学生的计算能力,属于基础题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 是函数
是函数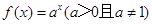 的图象上一点,数列
的图象上一点,数列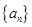 的前n项和
的前n项和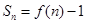 .
.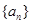 中,已知
中,已知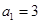 ,公比
,公比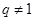 ,等差数列
,等差数列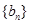 满足
满足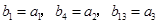 .
.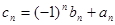 ,求数列
,求数列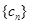 的前2n项和.
的前2n项和. 的首项
的首项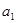 为a
为a ,设数列的前n项和为
,设数列的前n项和为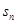 ,且
,且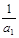 ,
,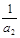 ,
,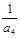 成等比数列.
成等比数列.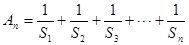 ,
,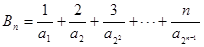 ,当
,当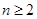 时,计算
时,计算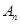 与
与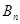 ,并比较
,并比较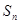 是等比数列
是等比数列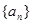 的前
的前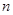 项和, 公比
项和, 公比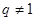 ,已知1是
,已知1是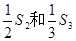 的等 差中项,6是
的等 差中项,6是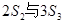 的等比中项,
的等比中项,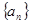 中,
中, 为常数,
为常数, ,且
,且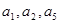 成公比不等于1的等比数列.
成公比不等于1的等比数列.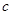 的值;
的值;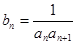 ,求数列
,求数列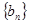 的前
的前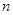 项和
项和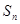 。
。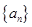 的各项均为正数,且
的各项均为正数,且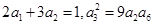
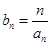 ,求数列
,求数列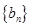 的前n项和
的前n项和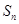 .
.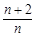 Sn(n=1,2,3…).
Sn(n=1,2,3…).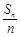 }是等比数列.
}是等比数列. 的前
的前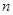 项和
项和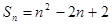 ,求通项公式
,求通项公式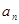 ;
;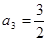 ,
,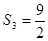 ,求通项公式
,求通项公式