题目内容
已知数列{an}中的相邻两项a2k-1,a2k是关于x的方程x2-(3k+2k)x+3k·2k=0的两个根,且a2k-1≤a2k(k=1,2,3,…).(1)求a1,a3,a5,a7;
(2)求数列{an}的前2n项和S2n;
(3)记f(n)=![]() (
(![]() +3),Tn=
+3),Tn=![]() +
+![]() +
+![]() +…+
+…+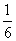 ,求证:
,求证:![]() ≤Tn≤
≤Tn≤![]() (n∈N*).
(n∈N*).
解:(1)方程x2-(3k+2k)x+3k·2k=0的两个根为x1=3k,x2=2k.
当k=1时,x1=3,x2=2,∴a1=2.
当k=2时,x1=6,x2=4,∴a3=4.
当k=3时,x1=9,x2=8,∴a5=8.
当k=4时,x1=12,x2=16,∴a7=12.
(2)S2n=a1+a2+…+a2n=(3+6+…+3n)+(2+22+…+2n)=![]() +2n+1-2.
+2n+1-2.
(3)Tn=![]() +
+![]() +…+
+…+![]() ,
,
∴T1=![]() =
=![]() ,T2=
,T2=![]() .
.
当n≥3时,
Tn=![]() +
+![]() +…≥
+…≥![]() ≥
≥![]() +
+![]() -(
-(![]() +…+
+…+![]() )
)
≥![]() +
+![]() (
(![]() +…+
+…+![]() )=
)=![]() +
+![]() >
>![]() .
.
同时Tn=![]() +…+
+…+![]() ≤
≤![]() +(
+(![]() +…+
+…+![]() )
)
≤![]() +
+![]() (
(![]() +…+
+…+![]() )=
)=![]()
![]() <
<![]() .
.
综上所述,当n∈N*时,![]() ≤Tn≤
≤Tn≤![]() .
.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目