题目内容
若椭圆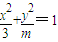
与直线x+2y-2=0有两个不同的交点，则m的取值范围是（ ）A．（
，3）B．（3，+∞）
C．（
，3）D．（
，3）∪（3，+∞）
【答案】分析：由椭圆
与直线x+2y-2=0联立，消去x并整理，根据椭圆与直线有两个不同的交点，建立不等式组，即可确定m的取值范围．
解答：解：由椭圆
与直线x+2y-2=0联立，消去x并整理得（3+4m）y2-8my+m=0．
根据条件椭圆
与直线x+2y-2=0有两个不同的交点，可得
，
解得
或m＞3．
故选D．
点评：本题考查直线与椭圆的位置关系，考查学生的计算能力，属于中档题．
与直线x+2y-2=0联立，消去x并整理，根据椭圆与直线有两个不同的交点，建立不等式组，即可确定m的取值范围．解答：解：由椭圆
与直线x+2y-2=0联立，消去x并整理得（3+4m）y2-8my+m=0．根据条件椭圆
与直线x+2y-2=0有两个不同的交点，可得，解得
或m＞3．故选D．
点评：本题考查直线与椭圆的位置关系，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
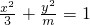与直线x+2y-2=0有两个不同的交点，则m的取值范围是
，3）
，3）
（a＞b＞0）过点A（0，2），离心率为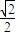
，过点A的直线l与椭圆交于另一点M．