题目内容
(本小题12分)椭圆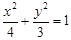 的左、右焦点分别为
的左、右焦点分别为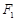 、
、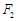 ,直线
,直线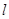 经过点
经过点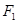 与椭圆交于
与椭圆交于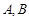 两点。
两点。
(1)求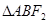 的周长;
的周长;
(2)若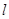 的倾斜角为
的倾斜角为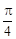 ,求
,求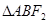 的面积。
的面积。
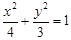 的左、右焦点分别为
的左、右焦点分别为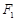 、
、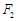 ,直线
,直线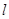 经过点
经过点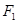 与椭圆交于
与椭圆交于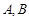 两点。
两点。(1)求
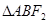 的周长;
的周长;(2)若
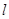 的倾斜角为
的倾斜角为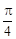 ,求
,求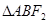 的面积。
的面积。(1) ,
, 的周长为
的周长为 。
。
(2) 。
。
 ,
, 的周长为
的周长为 。
。(2)
 。
。本题考查三角形周长的求法和三角形面积的计算,解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用椭圆的性质,注意椭圆定义、韦达定理在解题中的合理运用.
(1)由椭圆的定义,得AF1+AF2=2a,BF1+BF2=2a,又AF1+BF1=AB,所以,△ABF2的周长=AB+AF2+BF2=4a.再由a2=4,能导出△ABF2的周长.
(2)由F1(-1,0),AB的倾斜角为 ,知直线AB的方程为y=x+1.由
,知直线AB的方程为y=x+1.由 
消去x,得7y2-6y-9=0,设A(x1,y1),B(x2,y2),借助韦达定理能够求出△ABF2的面积.
解:(1)由椭圆的定义,得 ,
, , ----------2分
, ----------2分
又 ,所以
,所以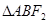 的周长为
的周长为 。--------4分
。--------4分
又因为 ,所以
,所以 ,故
,故 的周长为
的周长为 。-----------5分
。-----------5分
(2)由条件,得 ,因为
,因为 的倾斜角为
的倾斜角为 ,所以
,所以 斜率为
斜率为 ,
,
故直线 的方程为
的方程为 。-----------------6分
。-----------------6分
由 消去
消去 ,得
,得 , ------------------8分
, ------------------8分
设 ,解得
,解得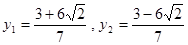 , -------------10分
, -------------10分
所以 。------------------12分
。------------------12分
(1)由椭圆的定义,得AF1+AF2=2a,BF1+BF2=2a,又AF1+BF1=AB,所以,△ABF2的周长=AB+AF2+BF2=4a.再由a2=4,能导出△ABF2的周长.
(2)由F1(-1,0),AB的倾斜角为
 ,知直线AB的方程为y=x+1.由
,知直线AB的方程为y=x+1.由 
| |
解:(1)由椭圆的定义,得
 ,
, , ----------2分
, ----------2分又
 ,所以
,所以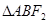 的周长为
的周长为 。--------4分
。--------4分又因为
 ,所以
,所以 ,故
,故 的周长为
的周长为 。-----------5分
。-----------5分(2)由条件,得
 ,因为
,因为 的倾斜角为
的倾斜角为 ,所以
,所以 斜率为
斜率为 ,
,故直线
 的方程为
的方程为 。-----------------6分
。-----------------6分由
 消去
消去 ,得
,得 , ------------------8分
, ------------------8分设
 ,解得
,解得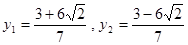 , -------------10分
, -------------10分所以
 。------------------12分
。------------------12分
练习册系列答案
相关题目
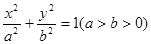 的左右焦点分别为
的左右焦点分别为 、
、 ,短轴两个端点为
,短轴两个端点为 、
、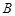 ,且四边形
,且四边形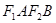 是边长为2的正方形。
是边长为2的正方形。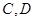 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点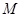 满足
满足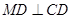 ,连接
,连接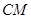 ,交椭圆于点
,交椭圆于点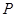 ;证明:
;证明: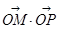 为定值;
为定值; 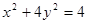 ,直线
,直线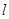 :y=x+m
:y=x+m 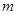 的值;
的值; ,若其焦点在
,若其焦点在 轴上,则
轴上,则 的取值范围是( )
的取值范围是( )



 过抛物线
过抛物线 的焦点,且与双曲线
的焦点,且与双曲线 有相同的焦点,则该椭圆的方程为: .
有相同的焦点,则该椭圆的方程为: .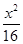 +
+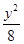 =1的离心率为( )
=1的离心率为( )


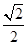
 的离心率为
的离心率为 ,并且直线
,并且直线 是抛物线
是抛物线 的一条切线。
的一条切线。 的动直线
的动直线 交椭圆
交椭圆 于
于 、
、 两点,试问:在直角坐标平面上是否存在一个定点
两点,试问:在直角坐标平面上是否存在一个定点 ,使得以
,使得以 为直径的圆恒过点
为直径的圆恒过点 的右焦点到直线
的右焦点到直线 的距离是
的距离是

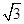
 的距离之和等于4,设点P的轨迹为C。
的距离之和等于4,设点P的轨迹为C。 与C交于A、B两点,k为何值时
与C交于A、B两点,k为何值时 ?
?