题目内容
(12分)若过定点A(2,0)的直线交椭圆 +y2=1于不同的两点E、F(点E在点A、F之间),且满足
+y2=1于不同的两点E、F(点E在点A、F之间),且满足 =m
=m ,求实数m的取值范围.
,求实数m的取值范围.
 +y2=1于不同的两点E、F(点E在点A、F之间),且满足
+y2=1于不同的两点E、F(点E在点A、F之间),且满足 =m
=m ,求实数m的取值范围.
,求实数m的取值范围. [ ,1)
,1)
 ,1)
,1)当直线EF斜率存在时,设直线EF的方程为y=kx+2,E(x1,y1),F(x2,y2),
代入椭圆方程得(1+2k2)x2+8kx+6=0,则x1+x2=- ,x1x2=
,x1x2= ,
,
由△>0解得k2> ,又由
,又由 =m
=m 得x1=mx2,则有
得x1=mx2,则有 ,
,
整理有(x1+x2)2= x1x2,则
x1x2,则 =
= ·
· ,
,
那么 =
= ,由k2>
,由k2> 可得12<
可得12< <16,即12<
<16,即12< <16,
<16,
由题知0<m<1,解得 <m<1;当直线EF斜率不存在时,其方程为x=0,从而
<m<1;当直线EF斜率不存在时,其方程为x=0,从而 =
=
 ,即m=
,即m= ;综上分析,实数m的取值范围为[
;综上分析,实数m的取值范围为[ ,1).
,1).
代入椭圆方程得(1+2k2)x2+8kx+6=0,则x1+x2=-
 ,x1x2=
,x1x2= ,
,由△>0解得k2>
 ,又由
,又由 =m
=m 得x1=mx2,则有
得x1=mx2,则有 ,
,整理有(x1+x2)2=
 x1x2,则
x1x2,则 =
= ·
· ,
, 那么
 =
= ,由k2>
,由k2> 可得12<
可得12< <16,即12<
<16,即12< <16,
<16,由题知0<m<1,解得
 <m<1;当直线EF斜率不存在时,其方程为x=0,从而
<m<1;当直线EF斜率不存在时,其方程为x=0,从而 =
=
 ,即m=
,即m= ;综上分析,实数m的取值范围为[
;综上分析,实数m的取值范围为[ ,1).
,1).
练习册系列答案
相关题目
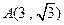 ,O为坐标原点,点
,O为坐标原点,点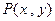 的坐标x,y满足
的坐标x,y满足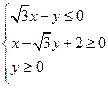 ,则向量
,则向量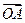 在向量
在向量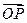 方向上的投影的取值范围是( )
方向上的投影的取值范围是( )



 ,
, ,
, ,
, .当
.当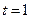 ,
, ,
, ,
, 时,分别求点
时,分别求点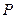 的坐标.
的坐标.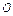 为
为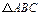 内一点,且
内一点,且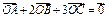 ,则
,则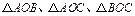 的面积之比等于
的面积之比等于
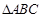 中,
中,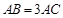 ,
,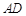 是
是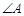 的平分线,且
的平分线,且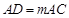 ,则实数
,则实数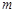 的取值范围是 ▲ .
的取值范围是 ▲ .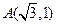 ,
,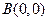 ,
,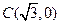 .设
.设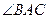 的平分线
的平分线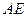 与
与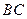 相交于
相交于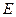 ,
,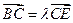 ,其中
,其中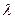 等于( )
等于( )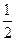
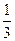
 、
、 的法向量分别为
的法向量分别为 =(2,3,5),
=(2,3,5), =(-3,1,-4),则
=(-3,1,-4),则 上的不同的三点,O是外一点,向量
上的不同的三点,O是外一点,向量 满足
满足 ,记
,记 .求函数
.求函数