题目内容
直线l过点P(-2,1)且斜率为k(k>1),将直线l绕P 点按逆时针方向旋转45°得到直线m,若直线l和m分别和y轴交于Q、R两点.
点按逆时针方向旋转45°得到直线m,若直线l和m分别和y轴交于Q、R两点.
(1)用k表示直线m的斜率;
(2)当k为何值时,△PQR的面积最小,并求面积最小时直线l的方程.
解:(1)设直线l的倾斜角为α,则直线m的倾斜角为α+45°,
故km=tan(45°+α)= =
= .
.
(2)由题意及(1)可知直线l:y-1=k(x+2),直线m:y-1= (x+2),故Q(0,2k+1),R
(x+2),故Q(0,2k+1),R .
.
∴|RQ|=|2k+1- |=2k+
|=2k+ +2
+2
=2(k-1)+ +4.
+4.
∴S△PQR= ×2×
×2×
=2(k-1)+ +4.
+4.
∵k>1,∴k-1>0,
∴S△PQR≥4 +4.
+4.
当且仅当2(k-1)= ,即k=
,即k= +1时等号成立,
+1时等号成立,
此时直线l方程为( +1)x-y+2
+1)x-y+2 +3=0.
+3=0.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
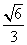 B.
B.
 D.
D.
 中,回归系数
中,回归系数 ( )
( ) 值范围是( )
值范围是( ) 或
或 <α<π
<α<π .
.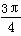 ,直线l1经过点A(3,2)、B(a,-1),且l1与l垂直,直线l2:2x
,直线l1经过点A(3,2)、B(a,-1),且l1与l垂直,直线l2:2x +by+1=0与直线l1平行,则a+
+by+1=0与直线l1平行,则a+
 D.
D.
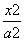 +
+ =1(a>b>0)的右焦点为F,过F的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,
=1(a>b>0)的右焦点为F,过F的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°, =2
=2 .
. C的离心率;
C的离心率;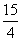 ,求椭圆C的方程.
,求椭圆C的方程.